题目内容
 已知如图的程序框图如图所示
已知如图的程序框图如图所示(1)写出程序框图所对应的算法语句;
(2)将右边的“直到型循环结构”改为“当型循环结构”,并写出当型循环相对应的算法语句.
考点:循环结构
专题:算法和程序框图
分析:程序进行判断前是否执行循环体,如果先执行循环体,则是直到型循环,否则是当型循环.解题的关键是弄清循环体是在判断框前还是后.
解答:
解:(1)算法语句如下:
s=0
i=2
Do
s=s+i
i=i+2
Loop While i<1000
PRINT s
END
(2)将右边的“直到型循环结构”改为“当型循环结构”,框图如下:

算法语句如下:
i=2
s=0
WHILE i>=1000
S=S+i
i=i+2
WEND
PRINT S
END
s=0
i=2
Do
s=s+i
i=i+2
Loop While i<1000
PRINT s
END
(2)将右边的“直到型循环结构”改为“当型循环结构”,框图如下:

算法语句如下:
i=2
s=0
WHILE i>=1000
S=S+i
i=i+2
WEND
PRINT S
END
点评:本题考察程序框图和算法,循环结构有两种形式:当型循环结构和直到型循环结构,当型循环是先判断后循环,直到型循环是先循环后判断,属于中档题.

练习册系列答案
相关题目
已知f(x)为R上的减函数,则满足f(2x-1)<f(1)的实数x的取值范围是 ( )
| A、(-∞,-1) |
| B、(-1,+∞) |
| C、(-∞,1) |
| D、(1,+∞) |
已知a,b,c分别为△ABC的三个内角A,B,C的对边,向量
=(
,-1),
=(cosA,sinA),若
⊥
,且acosB+bcosA=csinC,则B=( )
| m |
| 3 |
| n |
| m |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数y=f(x),x∈[a,b]的图象与直线x=2的交点的个数为( )
| A、1 | B、0 | C、1或0 | D、1或2 |
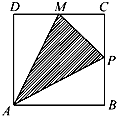 如图甲所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是图乙中的( )
如图甲所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是图乙中的( )