题目内容
求圆ρ=cosθ+2
sinθ圆心的极坐标 .
| 3 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把圆的极坐标方程化为直角坐标方程,求出圆心的直角坐标,再化为极坐标.
解答:
解:把圆ρ=cosθ+2
sinθ即 ρ2=ρcosθ+2
ρsinθ,化为直角坐标方程为 (x-
)2+(y-
)2=
,
表示以(
,
)为圆心的圆,故圆心的直角坐标为(
,
),化为极坐标为(
,arctan2
),
故答案为:(
,arctan2
).
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 13 |
| 4 |
表示以(
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
故答案为:(
| ||
| 2 |
| 3 |
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,点的直角坐标和极坐标的互化,属于基础题.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
数列{an}满足递推公式an=3an-1+3n-1(n≥2),又a1=5,则使得{
}为等差数列的实数λ=( )
| an+λ |
| 3n |
| A、2 | ||
| B、5 | ||
C、-
| ||
D、
|
18×17×16×…×9×8等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
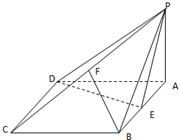 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.