题目内容
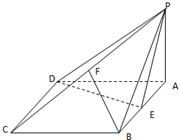 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.(Ⅰ)求证:BF∥面PDE;
(Ⅱ)求证:面PDE⊥面PAB.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)证明FG与BE平行且相等,可得BF∥GE,利用线面平行的判定可得BF∥面;
(Ⅱ)证明DE⊥AB,DE⊥AP,利用线面垂直的判定定理,可得DE⊥面PAB,从而可证面PDE⊥面PAB.
(Ⅱ)证明DE⊥AB,DE⊥AP,利用线面垂直的判定定理,可得DE⊥面PAB,从而可证面PDE⊥面PAB.
解答:
证明:画出图象,如图示:
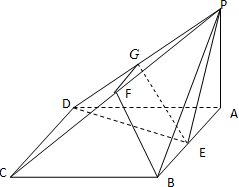 (Ⅰ)取PD的中点G,连结FG,GE,
(Ⅰ)取PD的中点G,连结FG,GE,
∵F,G是中点,∴FG∥CD且FG=
CD,∴FG与BE平行且相等,
∴BF∥GE,
∵GE?面PDE
∴BF∥面PDE.
(Ⅱ)∵底面ABCD是菱形,∠BCD=60°
∴△ABD为正三角形E是AB的中点,DE⊥AB,
∵PA⊥面ABCD,DE?面ABCD
∴DE⊥AP,
∵AB∩AP=A
∴DE⊥面PAB
∵DE?面PDE
∴面PDE⊥面PAB.
 (Ⅰ)取PD的中点G,连结FG,GE,
(Ⅰ)取PD的中点G,连结FG,GE,∵F,G是中点,∴FG∥CD且FG=
| 1 |
| 2 |
∴BF∥GE,
∵GE?面PDE
∴BF∥面PDE.
(Ⅱ)∵底面ABCD是菱形,∠BCD=60°
∴△ABD为正三角形E是AB的中点,DE⊥AB,
∵PA⊥面ABCD,DE?面ABCD
∴DE⊥AP,
∵AB∩AP=A
∴DE⊥面PAB
∵DE?面PDE
∴面PDE⊥面PAB.
点评:本题考查线面垂直,面面垂直,考查线面平行,正确运用判定定理是关键.

练习册系列答案
相关题目
自然数1,2,3,…,n按照一定的顺序排成一个数列:a1,a2,…,an.若满足|a1-1|+|a2-2|+…+|an-n|≤4,则称数列a1,a2,…,an为一个“优数列”.当n=6时,这样的“优数列”共有( )
| A、24个 | B、23个 |
| C、18个 | D、16个 |
已知数列{an}满足:a1=1,a2=a(a≤1),an+2=|an+1-an|,当a4=1时,a10的值为( )
| A、0 | B、1 | C、0或1 | D、±1 |