题目内容
15.定义符号函数:sgn(x)=$\left\{\begin{array}{l}{-1,x<0}\\{0,x=0}\\{1,x>0}\end{array}\right.$则函数f(x)=x•sgn(1nx)与函数g(x)=x4-x2的图象的交点个数为( )| A. | ,1 | B. | 2 | C. | 3 | D. | 0 |
分析 写出f(x)的解析式,令h(x)=g(x)-f(x),分段讨论h(x)的零点个数,
解答 解:f(x)=$\left\{\begin{array}{l}{-x,0<x<1}\\{0,x=1}\\{x,x>1}\end{array}\right.$,令h(x)=g(x)-f(x),
(1)当0<x<1时,h(x)=x4-x2+x=x(x3-x+1)=x(x(x2-1)+1),
∵0<x<1,∴-1<x2-1<0,∴-1<x(x2-1)<0,∴0<x(x2-1)+1<1,∴x(x(x2-1)+1)>0,即h(x)>0,
∴h(x)在(0,1)上无零点.
(2)当x=1时,h(x)=h(1)=g(1)-f(1)=0,∴x=1是h(x)的零点.
(3)当x>1时,h(x)=x4-x2-x,h′(x)=4x3-2x-1,h″(x)=12x2-2,∴当x>1时,h″(x)>0
∴h′(x)在(1,+∞)上是单调递增函数,∴hmin′(x)=h′(1)=1>0,∴h(x)在(1,+∞)上是单调递增函数,
∵h(1)=-1<0,∴h(x)在(1,+∞)上存在唯一一个零点.
综上,h(x)有两个零点,即f(x)与g(x)的图象有两个交点.
故选B.
点评 本题考查了分段函数的零点个数,导数与函数单调性的关系,属于中档题.

练习册系列答案
相关题目
5.已知三点A(3,5),B(x,7),C(-1,-3)在同一直线上,则x=( )
| A. | 2 | B. | -2 | C. | -4 | D. | 4 |
3.设函数f(x)=$\left\{\begin{array}{l}{2x+1,x<1}\\{{3}^{x},x≥1}\end{array}\right.$,则满足f(f(m))=3f(m)的实数m的取值范围是( )
| A. | (-∞,0)∪{-$\frac{1}{2}$} | B. | [0,1] | C. | [0,+∞)∪{-$\frac{1}{2}$} | D. | [1,+∞) |
7.已知点P(cosθ,sin2θ)和点Q(0,1)是两个相异点,则P、Q两点连线所在直线的倾斜角的取值范围为( )
| A. | [0,$\frac{π}{4}$] | B. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |
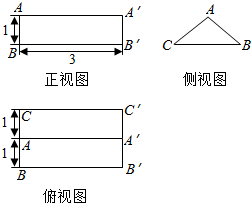 如图是一个几何体的三视图(单位:cm).
如图是一个几何体的三视图(单位:cm).