题目内容
为了解本市的交通状况，某校高一年级的同学分成了甲、乙、丙三个组，从下午13点到18点，分别对三个路口的机动车通行情况进行了实际调查，并绘制了频率分布直方图（如图），记甲、乙、丙三个组所调查数据的标准差分别为s1，s2，s3，则它们的大小关系为（ ）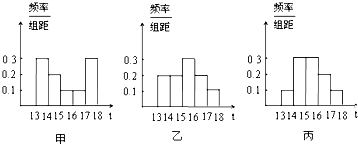
| A、s1＞s2＞s3 |
| B、s1＞s3＞s2 |
| C、s2＞s3＞s1 |
| D、s3＞s2＞s1 |
考点：频率分布直方图
专题：概率与统计
分析：根据频率分布直方图以及方差是描述数据波动大小的特征值，即数据波动性越大，方差就越大；由此判定甲、乙、丙三组数据方差的大小．
解答：
解：根据三个频率分布直方图，得
甲组数据的两端数字较大，绝大部分数字都处在两端，数据偏离平均数远，最分散，其方差最大；
乙组数据是单峰的，每一个小长方形的差别比较小，数字分布均匀，数据不如甲组偏离平均数大，
∴方差比甲组中数据的方差小；
丙组数据绝大部分数字都在平均数左右，数据最集中，∴方差最小；
综上，s1＞s2＞s3．
故选：A．
甲组数据的两端数字较大，绝大部分数字都处在两端，数据偏离平均数远，最分散，其方差最大；
乙组数据是单峰的，每一个小长方形的差别比较小，数字分布均匀，数据不如甲组偏离平均数大，
∴方差比甲组中数据的方差小；
丙组数据绝大部分数字都在平均数左右，数据最集中，∴方差最小；
综上，s1＞s2＞s3．
故选：A．
点评：本题考查了频率分布直方图和方差的问题，解题时应根据频率分布直方图得出数据，由方差的特征判定结果是什么，是基础题．
练习册系列答案
相关题目
已知x∈（0，
）且f（cosx）=sin
，则f（
）=（ ）
| π |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
命题“若函数f（x）=ex-mx在[0，+∞）上是减函数，则m＞1”的否命题是（ ）
| A、若函数f（x）=ex-mx在[0，+∞）上不是减函数，则m≤1 |
| B、若函数f（x）=ex-mx在[0，+∞）上是减函数，则m≤1 |
| C、若m＞1，则函数f（x）=ex-mx在[0，+∞）上是减函数 |
| D、若m≤1，则函数f（x）=ex-mx在[0，+∞）上不是减函数 |
“m=3”是“直线（m-1）x+2my+1=0与直线（m+3）x-（m-1）y+3=0相互垂直”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设Sn是等差数列{an}的前n项和，若
=1，则
=（ ）
| S11 |
| S9 |
| a6 |
| a5 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、
|
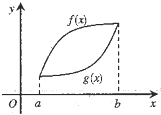已知函数f（x）和g（x）在区间[a，b]上的图象如图所示，那么下列说法正确的是（ ）| A、f（x）在a到b之间的平均变化率大于g（x）在a到b之间的平均变化率 |
| B、f（x）在a到b之间的平均变化率小于g（x）在a到b之间的平均变化率 |
| C、对于任意x0∈（a，b），函数f（x）在x=x0处的瞬时变化率总大于函数g（x）在x=x0处的瞬时变化率 |
| D、存在x0∈（a，b），使得函数f（x）在x=x0处的瞬时变化率小于函数g（x）在x=x0处的瞬时变化率 |
已知函数y=tan（ωx）（ω＞0）的最小正周期为2π，则函数y=ωcosx的值域是（ ）
| A、[-2，2] | ||||
| B、[-1，1] | ||||
C、[-
| ||||
D、[-
|