题目内容
已知函数y=tan(ωx)(ω>0)的最小正周期为2π,则函数y=ωcosx的值域是( )
| A、[-2,2] | ||||
| B、[-1,1] | ||||
C、[-
| ||||
D、[-
|
考点:三角函数的周期性及其求法,余弦函数的定义域和值域
专题:三角函数的图像与性质
分析:利用正切函数的周期公式可求得ω,利用余弦函数的性质即可求得y=
cosx的值域.
| 1 |
| 2 |
解答:
解:∵函数y=tan(ωx)(ω>0)的最小正周期为2π,
∴T=
=2π,
∴ω=
.
∴函数y=ωcosx=
cosx∈[-
,
],
∴函数y=
cosx的值域是[-
,
],
故选:D.
∴T=
| π |
| ω |
∴ω=
| 1 |
| 2 |
∴函数y=ωcosx=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴函数y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:D.
点评:本题考查正切函数的周期性及其求法,考查余弦函数的定义域和值域,求得ω=
是关键,属于中档题.
| 1 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若tan280°=a,则sin80°的结果为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、-
|
为了解本市的交通状况,某校高一年级的同学分成了甲、乙、丙三个组,从下午13点到18点,分别对三个路口的机动车通行情况进行了实际调查,并绘制了频率分布直方图(如图),记甲、乙、丙三个组所调查数据的标准差分别为s1,s2,s3,则它们的大小关系为( )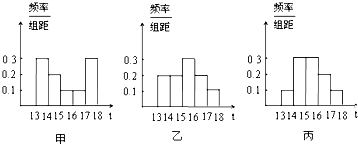

| A、s1>s2>s3 |
| B、s1>s3>s2 |
| C、s2>s3>s1 |
| D、s3>s2>s1 |
已知cosαcosβ=
,sin(
+α+β)=
,则sinαsinβ=( )
| 1 |
| 3 |
| π |
| 2 |
| 7 |
| 8 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若△ABC的三个顶点是A(-5,0),B(3,-3),C(0,2),则△ABC的面积为( )
A、
| ||
| B、31 | ||
| C、23 | ||
| D、46 |
以下程序运行结果为( )
t=1
For i=2 To 5
t=t*i
Next
输出t.
t=1
For i=2 To 5
t=t*i
Next
输出t.
| A、80 | B、95 |
| C、100 | D、120 |
要得到一个偶函数的图象,只需将函数f(x)=sin(x-
)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|