题目内容
“m=3”是“直线(m-1)x+2my+1=0与直线(m+3)x-(m-1)y+3=0相互垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:直线与圆,简易逻辑
分析:先求出直线(m+2)x+(1-m)y=0与直线(m-1)x+(2m+3)y+2=0相互垂直的等价条件,然后判断两个条件之间的充分性和必要性.
解答:
解:当m=3时,两直线方程分别为:2x+6m+1=0和6x-2y+3=0,此时两直线垂直.
若两直线垂直时,则有(m+3)(m-1)-2m(m-1)=0,
即(m-1)(3-m)=0,解得m=1或3.
∴“m=3”是“直线(m-1)x+2my+1=0与直线(m+3)x-(m-1)y+3=0相互垂直”的充分不必要条件.
故选:A.
若两直线垂直时,则有(m+3)(m-1)-2m(m-1)=0,
即(m-1)(3-m)=0,解得m=1或3.
∴“m=3”是“直线(m-1)x+2my+1=0与直线(m+3)x-(m-1)y+3=0相互垂直”的充分不必要条件.
故选:A.
点评:本题主要考查充分条件和必要条件的判断,利用直线垂直的等价条件是解决本题的关键,直线a1x+b1y+c1=0与a2x+b2y+c2=0垂直的条件为a1a2+b1b2=0.

练习册系列答案
相关题目
在△ABC中,a=2,b=
,A=
,则B等于( )
| 2 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题中,与命题“函数y=
的定义域为R”不等价的命题是( )
| ax2+bx+c |
| A、函数y=ax2+bx+c的最小值大于0 |
| B、不等式ax2+bx+c≥0对任意实数恒成立 |
| C、不存在x0∈R,使ax02+bx0+c<0 |
| D、函数y=ax2+bx+c的值域是[0,+∞)的子集 |
在△ABC中,已知B=60°,C=45°,BC=8,AD⊥BC于D,则AD长为( )
A、4(
| ||
B、4(
| ||
C、4(
| ||
D、4(3-
|
为了解本市的交通状况,某校高一年级的同学分成了甲、乙、丙三个组,从下午13点到18点,分别对三个路口的机动车通行情况进行了实际调查,并绘制了频率分布直方图(如图),记甲、乙、丙三个组所调查数据的标准差分别为s1,s2,s3,则它们的大小关系为( )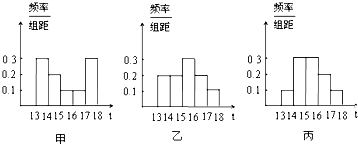

| A、s1>s2>s3 |
| B、s1>s3>s2 |
| C、s2>s3>s1 |
| D、s3>s2>s1 |
定义某种运算⊙,S=a⊙b,的运算原理如图所示,则式子6⊙3+2⊙4=( )


| A、16 | B、14 | C、10 | D、6 |
若△ABC的三个顶点是A(-5,0),B(3,-3),C(0,2),则△ABC的面积为( )
A、
| ||
| B、31 | ||
| C、23 | ||
| D、46 |