题目内容
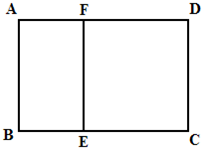 如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.(1)求出y关于x的函数解析式及x的取值范围;
(2)当x为何值时,围墙(包括EF)的修建总费用y最小?并求出y的最小值.
考点:基本不等式在最值问题中的应用,函数模型的选择与应用,不等式的实际应用
专题:应用题,不等式的解法及应用
分析:(1)根据面积确定AD的长,利用围墙(包括EF)的修建费用均为500元每平方米,即可求得函数的解析式;
(2)根据函数的特点,满足一正二定的条件,利用基本不等式,即可确定函数的最值.
(2)根据函数的特点,满足一正二定的条件,利用基本不等式,即可确定函数的最值.
解答:
解:(1)设AD=t米,则由题意得xt=2400,且t>x,故t=
>x,可得0<x<20
,…(4分)
则y=500(3x+2t)=500(3x+2×
),
所以y关于x的函数解析式为y=1500(x+
)(0<x<20
).
(2)y=1500(x+
)≥1500×2
=120000,
当且仅当x=
,即x=40时等号成立.
故当x为40米时,y最小.y的最小值为120000元.
| 2400 |
| x |
| 6 |
则y=500(3x+2t)=500(3x+2×
| 2400 |
| x |
所以y关于x的函数解析式为y=1500(x+
| 1600 |
| x |
| 6 |
(2)y=1500(x+
| 1600 |
| x |
x•
|
当且仅当x=
| 1600 |
| x |
故当x为40米时,y最小.y的最小值为120000元.
点评:本题考查函数模型的构建,考查基本不等式的运用,确定函数模型是关键.

练习册系列答案
相关题目
若变量x、y满足约束条件
,则z=2x+y的最大值是( )
|
| A、-2 | B、1 | C、3 | D、7 |
要得到函数y=sin(x+
)的图象,只需将函数y=sinx的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|