题目内容
已知数列{an}的前n项和为Sn,a1=1,an≠0,anan+1=4Sn-1
(1)求数列{an}的通项公式;
(2)设bn=
,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)设bn=
| 1 |
| anan+1 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由anan+1=4Sn-1,可得当n≥2时,an-1an=4Sn-1-1,an≠0,两式相减化为an+1-an-1=4,可得数列{an}的奇数项与偶数项分别为等差数列,进而得出;
(2)bn=
=
(
-
),利用“裂项求和”即可得出.
(2)bn=
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
解:(1)∵anan+1=4Sn-1,∴当n≥2时,an-1an=4Sn-1-1,anan+1-an-1an+1=4an,
∵an≠0,∴an+1-an-1=4,
当n=1时,a1a2=4a1-1,a1=1,解得a2=3,
∴数列{an}的奇数项与偶数项分别为等差数列,公差为4,首项分别为1,3.
∴当n=2k-1(k∈N*)为奇数时,an=a2k-1=1+4(k-1)=4k-3=2n-1;
当n=2k(k∈N*)为偶数时,an=a2k=3+4(k-1)=2n-1.
可得an=2n-1.
(2)bn=
=
=
(
-
),
∴数列{bn}的前n项和Tn=
[(1-
)+(
-
)+…+(
-
)]
=
(1-
)
=
.
∵an≠0,∴an+1-an-1=4,
当n=1时,a1a2=4a1-1,a1=1,解得a2=3,
∴数列{an}的奇数项与偶数项分别为等差数列,公差为4,首项分别为1,3.
∴当n=2k-1(k∈N*)为奇数时,an=a2k-1=1+4(k-1)=4k-3=2n-1;
当n=2k(k∈N*)为偶数时,an=a2k=3+4(k-1)=2n-1.
可得an=2n-1.
(2)bn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴数列{bn}的前n项和Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
=
| n |
| 2n+1 |
点评:本题考查了递推式的应用、等差数列的定义及其通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知实数x,y满足约束条件
,则z=
的最小值是( )
|
| 2x+y |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
,若f(x)在R上不单调,则实数a的取值范围是( )
|
| A、(-∞,4) |
| B、(0,4) |
| C、(-∞,0] |
| D、(4,+∞) |
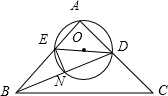 如图,在等腰△ABC中,AB=AC,D是AC的中点,DE平分∠ADB,交AB于E,过A,D,E的圆交BD于N,若AE=
如图,在等腰△ABC中,AB=AC,D是AC的中点,DE平分∠ADB,交AB于E,过A,D,E的圆交BD于N,若AE=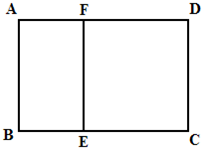 如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.