题目内容
若变量x、y满足约束条件
,则z=2x+y的最大值是( )
|
| A、-2 | B、1 | C、3 | D、7 |
考点:简单线性规划
专题:不等式的解法及应用
分析:由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.
解答:
解:由约束条件
作出可行域如图,

联立
,解得C(2,3),
化z=2x+y为y=-2x+z,由图可知,当直线y=-2x+z过C(2,3)时,直线在y轴上的截距最大,z有最大值为2×2+3=7.
故选:D.
|

联立
|
化z=2x+y为y=-2x+z,由图可知,当直线y=-2x+z过C(2,3)时,直线在y轴上的截距最大,z有最大值为2×2+3=7.
故选:D.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
已知函数f(x)=
,若f(x)在R上不单调,则实数a的取值范围是( )
|
| A、(-∞,4) |
| B、(0,4) |
| C、(-∞,0] |
| D、(4,+∞) |
下列直线方程中,不是圆x2+y2=5的切线方程的是( )
| A、x+2y+3=0 |
| B、2x-y-5=0 |
| C、2x-y+5=0 |
| D、x-2y+5=0 |
已知下列命题:
①命题“?x0∈R,x02+1>3x0”的否定是“?x∈R,x2+1<3x”;
②已知p、q为两个命题,若“p或q”为假命题,则“?p且?q为真命题”;
③“a>5”是“a>2”的充分不必要条件;
④“若xy=0,则x=0且y=0”的逆否命题为真命题.
其中所有真命题的序号是( )
①命题“?x0∈R,x02+1>3x0”的否定是“?x∈R,x2+1<3x”;
②已知p、q为两个命题,若“p或q”为假命题,则“?p且?q为真命题”;
③“a>5”是“a>2”的充分不必要条件;
④“若xy=0,则x=0且y=0”的逆否命题为真命题.
其中所有真命题的序号是( )
| A、①②③ | B、②④ | C、②③ | D、④ |
命题“事件A与事件B互斥”是命题“事件A与事件B对立”的( )
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
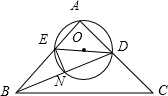 如图,在等腰△ABC中,AB=AC,D是AC的中点,DE平分∠ADB,交AB于E,过A,D,E的圆交BD于N,若AE=
如图,在等腰△ABC中,AB=AC,D是AC的中点,DE平分∠ADB,交AB于E,过A,D,E的圆交BD于N,若AE=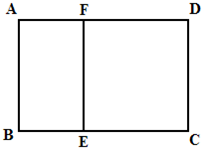 如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.