题目内容
已知函数y=x+
,x∈[1,3],其函数的最大值为 ,最小值 .
| 4 |
| x |
考点:基本不等式在最值问题中的应用
专题:计算题,导数的概念及应用
分析:利用导数确定函数的单调性,即可求出函数的最大值与最小值.
解答:
解:∵y=x+
,
∴y′=1-
,
∴y=x+
在[1,2]上单调递减,在[2,3]上单调递增,
∵x=1时,y=5;x=2时,y=4;x=3时,y=
,
∴函数y=x+
,x∈[1,3],其函数的最大值为5,最小值为4.
故答案为:5,4
| 4 |
| x |
∴y′=1-
| 4 |
| x2 |
∴y=x+
| 4 |
| x |
∵x=1时,y=5;x=2时,y=4;x=3时,y=
| 13 |
| 3 |
∴函数y=x+
| 4 |
| x |
故答案为:5,4
点评:本题考查利用导数求函数的最值,考查学生的计算能力,利用导数确定函数的单调性是关键.

练习册系列答案
相关题目
已知下列命题:
①命题“?x0∈R,x02+1>3x0”的否定是“?x∈R,x2+1<3x”;
②已知p、q为两个命题,若“p或q”为假命题,则“?p且?q为真命题”;
③“a>5”是“a>2”的充分不必要条件;
④“若xy=0,则x=0且y=0”的逆否命题为真命题.
其中所有真命题的序号是( )
①命题“?x0∈R,x02+1>3x0”的否定是“?x∈R,x2+1<3x”;
②已知p、q为两个命题,若“p或q”为假命题,则“?p且?q为真命题”;
③“a>5”是“a>2”的充分不必要条件;
④“若xy=0,则x=0且y=0”的逆否命题为真命题.
其中所有真命题的序号是( )
| A、①②③ | B、②④ | C、②③ | D、④ |
下列函数,在区间(
,π)上恒正且是增函数的是( )
| π |
| 2 |
| A、y=sinx |
| B、y=cosx |
| C、y=-sinx |
| D、y=-cosx |
已知复数z=
,则z-|z|对应的点所在的象限为( )
| 1 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
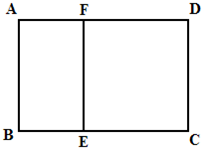 如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.