题目内容
现有10个数,它们能构成一个以l为首项,-3为公比的等比数列,若从这10个数中随机抽取一个数,则这个数大于8的概率是 .
考点:古典概型及其概率计算公式,等比数列的性质
专题:概率与统计
分析:由题意成等比数列的10个数为:1,-3,(-3)2,(-3)3…(-3)9,其中大于8的项有:(-3)2,(-3)4,(-3)6,(-3)8共4个数,由此能求出这10个数中随机抽取一个数,则它大于8的概率.
解答:
解:由题意成等比数列的10个数为:1,-3,(-3)2,(-3)3…(-3)9,
其中大于8的项有:(-3)2,(-3)4,(-3)6,(-3)8共4个数,
这10个数中随机抽取一个数,则它大于8的概率是P=
=
.
故答案为:
.
其中大于8的项有:(-3)2,(-3)4,(-3)6,(-3)8共4个数,
这10个数中随机抽取一个数,则它大于8的概率是P=
| 4 |
| 10 |
| 2 |
| 5 |
故答案为:
| 2 |
| 5 |
点评:本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
已知函数f(x)=x2的图象上一点(1,1)及邻近一点(1+△x,1+△y),则
等于( )
| △y |
| △x |
| A、2 |
| B、2+△x |
| C、2+2△x |
| D、2△x+(△x)2 |
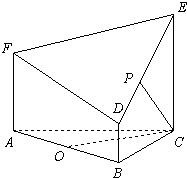 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,AB=2,BD=1,AF=a.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,AB=2,BD=1,AF=a.