题目内容
设集合A={a，b}，B={a+1，5}，若A∩B={2}，则A∪B= ．
考点：交集及其运算
专题：集合
分析：由A与B的交集，得到元素2属于A，属于B，进而求出a的值，确定出A与B，求出两集合的并集即可．
解答：
解：∵A={a，b}，B={a+1，5}，且A∩B={2}，
∴2∈A，2∈B，
∴a+1=2，即a=1，b=2，
∴A={1，2}，B={2，5}，
则A∪B={1，2，5}．
故答案为：{1，2，5}
∴2∈A，2∈B，
∴a+1=2，即a=1，b=2，
∴A={1，2}，B={2，5}，
则A∪B={1，2，5}．
故答案为：{1，2，5}
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
如果角θ的终边经过点P（-
，
），那么tanθ等于（ ）
| ||
| 2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
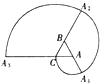如图，一条螺旋线是用以下方法画成的：△ABC是边长为1的正三角形，曲线CA1，A1A2，A2A3是分别以A、B、C为圆心，AC、BA1、CA2为半径画的圆弧，曲线CA1A2A3称为螺旋线的第一圈，然后又以A为圆心，AA3为半径画圆弧…这样画到第n圈，则所得螺旋线的长度ln为（ ）| A、（3n2+n）π | ||
| B、（3n2-n+1）π | ||
C、
| ||
D、
|
若a＞b＞0，且a+b=1，则下列式子中最大的是（ ）
| A、log2a+log2b+1 |
| B、log2a |
| C、log2（a2+b2） |
| D、-1 |