题目内容
已知函数f(x)满足2f(x+2)=f(x),当x∈(0,2)时,f(x)=lnx+ax(a<-
),当x∈(-4,-2)时,f(x)的最大值为-4.求x∈(0,2)时f(x)的解析式.
| 1 |
| 2 |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:由已知得:f(x)=2f(x+2)=4f(x+4),设x∈(-4,-2)时,则x+4∈(0,2),代入x∈(0,2)时,f(x)=lnx+ax(a<-
),求出f(x+4)=ln(x+4)+a(x+4),再根据当x∈(-4,-2)时,f(x)的最大值为-4,利用导数求得它的最大值,解方程即可求得a的值,进而求得结论;
| 1 |
| 2 |
解答:
解:由已知得:f(x)=2f(x+2)=4f(x+4),
∵x∈(0,2)时,f(x)=lnx+ax(a<-
),设x∈(-4,-2)时,则x+4∈(0,2),
∴f(x+4)=ln(x+4)+a(x+4)
∴x∈(-4,-2)时,f(x)=4f(x+4)=4ln(x+4)+4a(x+4)
f′(x)=
+4a=4a•
,
∵a<-
,
∴-4<-
-4<-2
∴当x∈(-4,-
-4)时,f′(x)>0,f(x)为增函数,
当x∈(-
-4,2)时,f′(x)<0,f(x)为减函数,
当x=-
-4时,f(x)有最大值4ln(-
)+a(-
)
4ln(-
)+a(-
)=-4,
解得a=-1
∴当x∈(0,2)时,f(x)=lnx-x
∵x∈(0,2)时,f(x)=lnx+ax(a<-
| 1 |
| 2 |
∴f(x+4)=ln(x+4)+a(x+4)
∴x∈(-4,-2)时,f(x)=4f(x+4)=4ln(x+4)+4a(x+4)
f′(x)=
| 4 |
| x+4 |
x+4+
| ||
| x+4 |
∵a<-
| 1 |
| 2 |
∴-4<-
| 1 |
| a |
∴当x∈(-4,-
| 1 |
| a |
当x∈(-
| 1 |
| a |
当x=-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
4ln(-
| 1 |
| a |
| 1 |
| a |
解得a=-1
∴当x∈(0,2)时,f(x)=lnx-x
点评:此题是个难题.考查函数解析式的求法以及函数恒成立问题,体现了转化和分类讨论的思想方法,其中问题(2)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知α∈(
,π),且cosα=-
,则sinα=( )
| π |
| 2 |
| 3 |
| 5 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
某校高二年级文科共303名学生,为了调查情况,学校决定随机抽取50人参加抽测,采取先简单随机抽样去掉3人然后系统抽样抽取出50人的方式进行.则在此抽样方式下,某学生甲被抽中的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
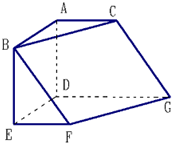 在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形ABED是矩形,四边形ADGC是直角梯形,∠ADG=90°,四边形DEFG是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.
在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形ABED是矩形,四边形ADGC是直角梯形,∠ADG=90°,四边形DEFG是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.