题目内容
两艘轮船都有停靠同一个泊位，它们可能在一昼夜的任意时刻到达．甲、乙两船停靠泊位的时间都是6小时，求一艘船停靠泊位时必须等待一段时间的概率．
考点：几何概型
专题：计算题,概率与统计
分析：设出甲、乙到达的时刻，列出所有基本事件的约束条件同时列出这两艘船中至少有一艘在停靠泊位时必须等待约束条件，利用线性规划作出平面区域，利用几何概型概率公式求出概率．
解答：
解：设甲船到达的时间为x，乙船到达的时间为y则0≤x，y＜24；
若至少有一艘在停靠泊位时必须等待，则0＜y-x＜6或0＜x-y＜6
如图：
必须等待的概率为：1-
=
．
若至少有一艘在停靠泊位时必须等待，则0＜y-x＜6或0＜x-y＜6
如图：
必须等待的概率为：1-
| 182 |
| 242 |
| 7 |
| 16 |
点评：本题主要考查建模、解模能力；解答关键是利用线性规划作出事件对应的平面区域，再利用几何概型概率公式求出事件的概率．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
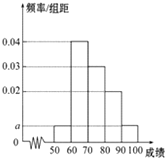某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]
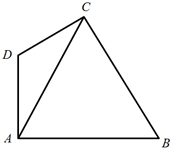某游乐园拟建一主题游戏园，该游戏园为四边形区域ABCD，其中三角形区域ABC为主题活动园区，∠ACB=60°；AD、CD为游客通道（不考虑宽度），通道AD、CD围成三角形区域ADC为游客休闲中心，供游客休憩．定义在R上的函数f（x）满足f（x）=
，则f（2015）=（ ）
|
| A、-1 | B、0 | C、1 | D、2 |
“a＞b，c＞d”是“a+c＞b+d”的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |