题目内容
已知函数y=f（x）是定义在R上的单调函数，对?x∈R，f[f（x）-2x]=3恒成立，则f（3）=（ ）
| A、1 | B、3 | C、8 | D、9 |
考点：函数恒成立问题
专题：函数的性质及应用
分析：先根据函数的单调性与恒成立，求出函数的解析式即可．
解答：
解：因为函数y=f（x）是定义在R上的单调函数，对?x∈R，f[f（x）-2x]=3恒成立
所以存在常数c，使得f（c）=3，
∴f（x）-2x=c，∴f（x）=2x+c，又f（c）=3，∴2c+c=3，
∴c=1，∴f（x）=2x+1，∴f（3）=9
故答案为：D
所以存在常数c，使得f（c）=3，
∴f（x）-2x=c，∴f（x）=2x+c，又f（c）=3，∴2c+c=3，
∴c=1，∴f（x）=2x+1，∴f（3）=9
故答案为：D
点评：本题考查了恒成立的思想，以及函数单调性，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
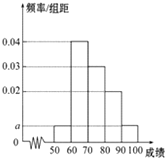某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]
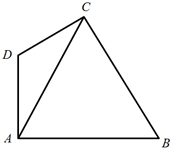某游乐园拟建一主题游戏园，该游戏园为四边形区域ABCD，其中三角形区域ABC为主题活动园区，∠ACB=60°；AD、CD为游客通道（不考虑宽度），通道AD、CD围成三角形区域ADC为游客休闲中心，供游客休憩．“a＞b，c＞d”是“a+c＞b+d”的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |