题目内容
已知函数g(x)是R上的奇函数,且当x<0时g(x)=-ln(1-x),设函数f(x)=
,若f(2-x2)>f(x),则实数x的取值范围是( )
|
| A、(-∞,1)∪(2,+∞) |
| B、(-∞,-2)∪(1,+∞) |
| C、(1,2) |
| D、(-2,1) |
考点:奇偶性与单调性的综合
专题:综合题,函数的性质及应用
分析:先由函数g(x)是奇函数,求出函数g(x)的解析式,再利用f(x)与g(x)的关系得到f(x)的单调性,利用函数单调性解不等式f(2-x2)>f(x),求出实数x的取值范围.
解答:
解:∵函数g(x)是R上的奇函数,且当x<0时,g(x)=-ln(1-x),
∴当x>0时,g(x)=-g(-x)=-[-ln(1+x)]=ln(1+x).
∵函数f(x)=
,
∴当x≤0时,f(x)=x3为单调递增函数,值域(-∞,0].
当x>0时,f(x)=lnx为单调递增函数,值域(0,+∞).
∴函数f(x)在区间(-∞,+∞)上单调递增.
∵f(2-x2)>f(x),
∴2-x2>x,
即x2+x-2<0,
∴(x+2)(x-1)<0,
∴-2<x<1.
∴x∈(-2,1).
故选:D.
∴当x>0时,g(x)=-g(-x)=-[-ln(1+x)]=ln(1+x).
∵函数f(x)=
|
∴当x≤0时,f(x)=x3为单调递增函数,值域(-∞,0].
当x>0时,f(x)=lnx为单调递增函数,值域(0,+∞).
∴函数f(x)在区间(-∞,+∞)上单调递增.
∵f(2-x2)>f(x),
∴2-x2>x,
即x2+x-2<0,
∴(x+2)(x-1)<0,
∴-2<x<1.
∴x∈(-2,1).
故选:D.
点评:本题考查了奇函数的解析式求法、分段函数的单调性研究、函数单调性的应用,属于中档题,确定函数f(x)在区间(-∞,+∞)上单调递增是关键.

练习册系列答案
相关题目
已知a,b,c,d是四条不重合的直线,其中c为a在平面α上的射影,d为b在平面α上的射影,则( )
| A、c∥d⇒a∥b |
| B、a⊥b⇒c⊥d |
| C、a∥b⇒c∥d |
| D、c⊥d⇒a⊥b |
定义在R上的函数f(x)满足f(x)=
,则f(2015)=( )
|
| A、-1 | B、0 | C、1 | D、2 |
在△ABC中,角A、B、C的对边分别为a,b,c,a=1,b=
,∠A=
则∠B等于( )
| 3 |
| π |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
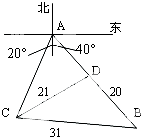 观测站C处在目标A的南偏西20°方向,从A出发有一条南偏东40°走向的公路,在C处观测到与C相距31km公路上的B处有一人正沿此公路向A走去,走20km到达D处,此时测得CD距离21km,求此人在D处距A还有多远?
观测站C处在目标A的南偏西20°方向,从A出发有一条南偏东40°走向的公路,在C处观测到与C相距31km公路上的B处有一人正沿此公路向A走去,走20km到达D处,此时测得CD距离21km,求此人在D处距A还有多远?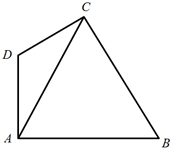 某游乐园拟建一主题游戏园,该游戏园为四边形区域ABCD,其中三角形区域ABC为主题活动园区,∠ACB=60°;AD、CD为游客通道(不考虑宽度),通道AD、CD围成三角形区域ADC为游客休闲中心,供游客休憩.
某游乐园拟建一主题游戏园,该游戏园为四边形区域ABCD,其中三角形区域ABC为主题活动园区,∠ACB=60°;AD、CD为游客通道(不考虑宽度),通道AD、CD围成三角形区域ADC为游客休闲中心,供游客休憩.