题目内容
函数f（x）=2x2-mx+3，在（-∞，-2]上是减函数，在[-2，+∞）上是增函数，则f（1）= ．
考点：二次函数的性质
专题：函数的性质及应用
分析：先求出函数的对称轴，解出m的值，求出解析式，进而求出f（1）的值．
解答：
解：∵函数f（x）在（-∞，-2]上是减函数，在[-2，+∞）上是增函数，
∴对称轴x=-2=
，解得：m=-8，
∴f（x）=2x2+8x+3，
∴f（1）=13，
故答案为：13．
∴对称轴x=-2=
| m |
| 4 |
∴f（x）=2x2+8x+3，
∴f（1）=13，
故答案为：13．
点评：本题考查了二次函数的性质，函数的单调性，对称性，是一道基础题．
练习册系列答案
导学全程练创优训练系列答案
相关题目
已知定义域为R的函数f （x）满足对任意的x1，x2∈（8，+∞）（x1＜x2），有f（x1）＞f（x2），且函数y=f（x+8）为偶函数，则（ ）
| A、f （6）＞f （7） |
| B、f （6）＞f （9） |
| C、f （7）＞f （9） |
| D、f （7）＞f （10） |
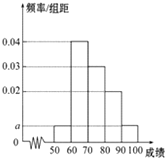某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]
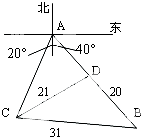观测站C处在目标A的南偏西20°方向，从A出发有一条南偏东40°走向的公路，在C处观测到与C相距31km公路上的B处有一人正沿此公路向A走去，走20km到达D处，此时测得CD距离21km，求此人在D处距A还有多远？
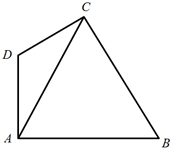某游乐园拟建一主题游戏园，该游戏园为四边形区域ABCD，其中三角形区域ABC为主题活动园区，∠ACB=60°；AD、CD为游客通道（不考虑宽度），通道AD、CD围成三角形区域ADC为游客休闲中心，供游客休憩．