题目内容
集合M={x|x=
+
，k∈Z}，N={x|x=
+
，k∈Z}，则（ ）
| kπ |
| 2 |
| π |
| 4 |
| kπ |
| 4 |
| π |
| 2 |
| A、M=N | B、M?N |
| C、M?N | D、M∩N=∅ |
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：判断集合M、N的关系要分两步，即M是不是N的子集，N是不是M的子集，利用子集的定义完成即可．
解答：
解：∵
∈N，但
∉M，
∴N不是M的子集，
又∵?a∈M，
则a=
+
，k∈Z，
则a=
+
，
∵2k-1∈Z，
则a∈N，
则M?N．
故选C．
| π |
| 2 |
| π |
| 2 |
∴N不是M的子集，
又∵?a∈M，
则a=
| kπ |
| 2 |
| π |
| 4 |
则a=
| (2k-1)π |
| 4 |
| π |
| 2 |
∵2k-1∈Z，
则a∈N，
则M?N．
故选C．
点评：本题考查了集合之间的包含关系，判断两个集合的关系要分两步，即分别说明二者之间是不是子集，不是常用反例法，是要利用子集的定义完成．
练习册系列答案
互动英语系列答案
相关题目
若ax2+bx+c＜0的解集为{x|x＜-2或x＞4}，则对于函数f（x）=ax2+bx+c应有（ ）
| A、f（5）＜f（2）＜f（-1） |
| B、f（5）＜f（-1）＜f（2） |
| C、f（-1）＜f（2）＜f（5） |
| D、f（2）＜f（-1）＜f（5） |
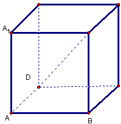
如图，在正方体ABCD-A1B1C1D1中，异面直线DB1与BC1的所成角为（ ）
| A、60° | B、30° |
| C、90° | D、45° |
变换
=
的几何意义为（ ）
|
|
|
| A、关于y轴反射变换 |
| B、关于x轴反射变换 |
| C、关于原点反射变换 |
| D、以上都不对 |
在区间[0，1]上任取一个实数x，则事件“sinπx≥
”发生的概率是（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某单位为了提高员工素质，举办了一场跳绳比赛，其中男员工12人，女员工18人，其成绩编成如图所示的茎叶图（单位：分），分数在175分以上（含175分）者定为“运动健将”，并给予特别奖励，其他人员则给予“运动积极分子”称号．