题目内容
变换
=
的几何意义为（ ）
|
|
|
| A、关于y轴反射变换 |
| B、关于x轴反射变换 |
| C、关于原点反射变换 |
| D、以上都不对 |
考点：反射变换
专题：矩阵和变换
分析：在坐标系xoy内，
经过变换后变为
，由此能求出结果．
|
|
解答：
解：在坐标系xoy内，
经过变换后变为
，
二者关于x轴对称，
所以变换
=
的几何意义为关于x轴的反射变换．
故选：B．
|
|
二者关于x轴对称，
所以变换
|
|
|
故选：B．
点评：本题考查反射变换的应用，是基础题，解题时要认真审题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
计箅cos42°cos18°-cos48°sin18°的结果等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某流程图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
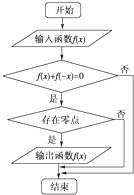
| A、f（x）=sinx | ||
| B、f（x）=cosx | ||
C、f（x）=
| ||
| D、f（x）=x2 |
将函数f（x）=sinx+cosx的图象向左平移φ（φ＞0）个单位长度，所得图象关于原点对称，则φ的最小值为（ ）
A、-
| ||
B、
| ||
C、
| ||
D、
|
已知（x，y）满足
，则k=
的最大值等于（ ）
|
| y |
| x+1 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
极坐标方程ρcos2θ=4sin θ所表示的曲线是（ ）
| A、一条直线 | B、一个圆 |
| C、一条抛物线 | D、一条双曲线 |
集合M={x|x=
+
，k∈Z}，N={x|x=
+
，k∈Z}，则（ ）
| kπ |
| 2 |
| π |
| 4 |
| kπ |
| 4 |
| π |
| 2 |
| A、M=N | B、M?N |
| C、M?N | D、M∩N=∅ |