题目内容
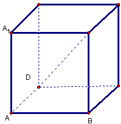
如图，在正方体ABCD-A1B1C1D1中，异面直线DB1与BC1的所成角为（ ）
| A、60° | B、30° |
| C、90° | D、45° |
考点：异面直线及其所成的角
专题：计算题,空间角
分析：连接B1C，由线面垂直的性质，得到CD⊥BC1，再由正方形的性质得到B1C⊥BC1，再由线面垂直的判断即可得到BC1⊥平面CDB1，从而BC1⊥DB1．
解答：
解：连接B1C，
∵CD⊥平面BCC1B1，∴CD⊥BC1，
∵B1C⊥BC1，
又CD，B1C相交，
∴BC1⊥平面CDB1，
∴BC1⊥DB1，
故异面直线DB1与BC1的所成角为90°．
故选C．
解：连接B1C，∵CD⊥平面BCC1B1，∴CD⊥BC1，
∵B1C⊥BC1，
又CD，B1C相交，
∴BC1⊥平面CDB1，
∴BC1⊥DB1，
故异面直线DB1与BC1的所成角为90°．
故选C．
点评：本题考查空间异面直线所成的角，考查线面垂直的判定和性质定理的运用，考查空间想象能力和推理能力，属于基础题．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
设a，b∈R，且i（a+i）=b-i，则a-b=（ ）
| A、2 | B、1 | C、0 | D、-2 |
某流程图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
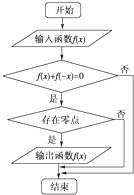
| A、f（x）=sinx | ||
| B、f（x）=cosx | ||
C、f（x）=
| ||
| D、f（x）=x2 |
已知直线m，n和平面α，那么m∥n的一个充分但非必要条件是（ ）
| A、m∥α，n∥α |
| B、m⊥α，n⊥α |
| C、m∥α，且n?α |
| D、m，n与α成等角 |
将函数f（x）=sinx+cosx的图象向左平移φ（φ＞0）个单位长度，所得图象关于原点对称，则φ的最小值为（ ）
A、-
| ||
B、
| ||
C、
| ||
D、
|
已知（x，y）满足
，则k=
的最大值等于（ ）
|
| y |
| x+1 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
集合M={x|x=
+
，k∈Z}，N={x|x=
+
，k∈Z}，则（ ）
| kπ |
| 2 |
| π |
| 4 |
| kπ |
| 4 |
| π |
| 2 |
| A、M=N | B、M?N |
| C、M?N | D、M∩N=∅ |