题目内容
若ax2+bx+c<0的解集为{x|x<-2或x>4},则对于函数f(x)=ax2+bx+c应有( )
| A、f(5)<f(2)<f(-1) |
| B、f(5)<f(-1)<f(2) |
| C、f(-1)<f(2)<f(5) |
| D、f(2)<f(-1)<f(5) |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:由于ax2+bx+c<0的解集为{x|x<-2或x>4},可知;-2,4是ax2+bx+c=0的两个实数根,且a<0.得到
=-2,
=-8.因此函数f(x)=ax2+bx+c=a(x2+
x+
)=a(x-1)2-9a.可知:a<0,抛物线开口向下,且对称轴为x=1.当x≥1时,函数f(x)单调递减.即可得出.
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
解答:
解:∵ax2+bx+c<0的解集为{x|x<-2或x>4},
∴-2,4是ax2+bx+c=0的两个实数根,且a<0.
∴-2+4=-
,-2×4=
.
化为
=-2,
=-8.
∴函数f(x)=ax2+bx+c=a(x2+
x+
)=a(x2-2x-8)=a(x-1)2-9a.
∵a<0,抛物线开口向下,且对称轴为x=1.
∴当x≥1时,函数f(x)单调递减,
∴f(5)<f(3)<f(2),f(3)=f(-1),
∴f(5)<f(-1)<f(2).
故选:B.
∴-2,4是ax2+bx+c=0的两个实数根,且a<0.
∴-2+4=-
| b |
| a |
| c |
| a |
化为
| b |
| a |
| c |
| a |
∴函数f(x)=ax2+bx+c=a(x2+
| b |
| a |
| c |
| a |
∵a<0,抛物线开口向下,且对称轴为x=1.
∴当x≥1时,函数f(x)单调递减,
∴f(5)<f(3)<f(2),f(3)=f(-1),
∴f(5)<f(-1)<f(2).
故选:B.
点评:本题考查了一元二次不等式的解集与相应的一元二次方程的实数根之间的关系、二次函数的图象与性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
一个几何体的正视图为一个四边形,则这个几何体可能是下列几何体中的( )
①圆锥 ②圆柱 ③三棱锥 ④四棱柱.
①圆锥 ②圆柱 ③三棱锥 ④四棱柱.
| A、①② | B、②③ | C、①④ | D、②④ |
计箅cos42°cos18°-cos48°sin18°的结果等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若变量x,y满足约束条件
且z=2x+y的最大值和最小值分别为m和n,则m+n=( )
|
| A、6 | B、-6 | C、0 | D、1 |
函数f(x)=
的定义域为( )
log
|
| A、(-∞,1] | ||
| B、[1,+∞) | ||
C、(
| ||
D、(
|
设a,b∈R,且i(a+i)=b-i,则a-b=( )
| A、2 | B、1 | C、0 | D、-2 |
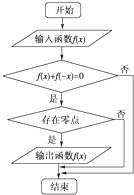
某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )

| A、f(x)=sinx | ||
| B、f(x)=cosx | ||
C、f(x)=
| ||
| D、f(x)=x2 |
集合M={x|x=
+
,k∈Z},N={x|x=
+
,k∈Z},则( )
| kπ |
| 2 |
| π |
| 4 |
| kπ |
| 4 |
| π |
| 2 |
| A、M=N | B、M?N |
| C、M?N | D、M∩N=∅ |