题目内容
是否存在角α和β,当α∈(-
,
),β∈(0,π)时,等式
同时成立?若存在,则求出α和β的值;若不存在,请说明理由.
| π |
| 2 |
| π |
| 2 |
|
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:首先由诱导公式简化已知条件并列方程组,再利用公式sin2β+cos2β=1解方程组,最后根据特殊角三角函数值求出满足要求的α、β.
解答:
解 存在α=
,β=
使等式同时成立.理由如下:
由由条件得
,
两式平方相加得,sin2α+3cos2α=2,∴cos2α=
即cosα=±
.
∵α∈(-
,
),∴α=
或α=-
.
将α=
代入②得cosβ=
.又β∈(0,π),
∴β=
,代入①可知,符合.
将α=-
代入②得β=
,代入①可知,不符合.
综上可知α=
,β=
.
| π |
| 4 |
| π |
| 6 |
由由条件得
|
两式平方相加得,sin2α+3cos2α=2,∴cos2α=
| 1 |
| 2 |
| ||
| 2 |
∵α∈(-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
将α=
| π |
| 4 |
| ||
| 2 |
∴β=
| π |
| 6 |
将α=-
| π |
| 4 |
| π |
| 6 |
综上可知α=
| π |
| 4 |
| π |
| 6 |
点评:本题综合考查诱导公式、同角正余弦关系式及特殊角三角函数值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
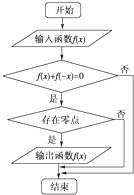

| A、f(x)=sinx | ||
| B、f(x)=cosx | ||
C、f(x)=
| ||
| D、f(x)=x2 |
集合M={x|x=
+
,k∈Z},N={x|x=
+
,k∈Z},则( )
| kπ |
| 2 |
| π |
| 4 |
| kπ |
| 4 |
| π |
| 2 |
| A、M=N | B、M?N |
| C、M?N | D、M∩N=∅ |
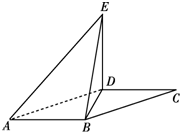 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4.将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4.将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.