题目内容
在△ABC中,∠B=60°,AC=
,求AB+BC的取值范围.
| 3 |
考点:正弦定理
专题:解三角形
分析:由条件利用正弦定理可得AB+BC2sinC+2sinA=2
cos(60°-A),结合60°-A的范围,以及余弦函数的值域,求得AB+BC的取值范围.
| 3 |
解答:
解:△ABC中,∠B=60°,AC=
,设三角形外接圆的直径为2r,
则由正弦定理可得2r=
=
=2,AB+BC=2sinC+2sinA=2[sin(120°-A)+sinA]
=4sin60°cos(60°-A)=2
cos(60°-A).
∵-60°<60°-A<60°,∴1≥cos(60°-A)>
,2
≥2
cos(60°-A)>
,
即 AB+BC的取值范围为(
,2
].
| 3 |
则由正弦定理可得2r=
| b |
| sinB |
| ||||
|
=4sin60°cos(60°-A)=2
| 3 |
∵-60°<60°-A<60°,∴1≥cos(60°-A)>
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
即 AB+BC的取值范围为(
| 3 |
| 3 |
点评:本题主要考查正弦定理的应用以及辅助角公式的应用.解决这类问题的关键在于对公式的熟练掌握以及灵活运用,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
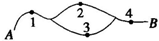 如图所示,在A、B间有四个焊接点1,2,3,4,若焊接点脱落导致断路,则电路,则电路不通,今发现A、B之间电路不通,则焊点脱落的不同情况有( )
如图所示,在A、B间有四个焊接点1,2,3,4,若焊接点脱落导致断路,则电路,则电路不通,今发现A、B之间电路不通,则焊点脱落的不同情况有( )| A、9种 | B、11种 |
| C、13种 | D、15种 |
已知角α的终边经过点P0(-3,-4),则cos(
+α)的值为( )
| π |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
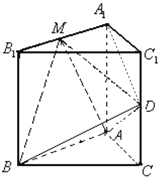 (文)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC=
(文)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC=