题目内容
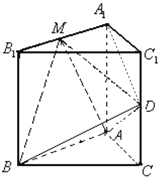 (文)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC=
(文)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC=| π |
| 4 |
(1)当M为A1B1中点时,求异面直线DM与AB所成角的大小.
(2)指出直线CC1与平面MAB的位置关系(不用证明),并求三棱锥D-MAB的体积.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(1)根据AB∥A1B1,可得∠A1MD或其补角是异面直线DM与AB所成的角;
(2)CC1∥平面MAB.确定D到平面AA1B1B的距离与C到平面AA1B1B的距离相等,为CA=1,求出△MAB的面积,即可求三棱锥D-MAB的体积.
(2)CC1∥平面MAB.确定D到平面AA1B1B的距离与C到平面AA1B1B的距离相等,为CA=1,求出△MAB的面积,即可求三棱锥D-MAB的体积.
解答:
解:(1)∵AB∥A1B1
∴∠A1MD或其补角是异面直线DM与AB所成的角.…3分
连接A1D,则三角形A1DM为直角三角形,且∠DA1M=900,A1D=
,A1M=
∴tan∠A1MD=
=
…5分
∴异面直线DM与AB所成的角为arctan
.…6分
(2)CC1∥平面AA1B1B即CC1∥平面MAB(不必证明)…7分
∵CA⊥AB,CA⊥AA1,AB∩AA1=A,
∴CA⊥平面AA1B1B
∴C到平面AA1B1B的距离为CA=1.
∵CC1∥平面AA1B1B,
可知D到平面AA1B1B的距离与C到平面AA1B1B的距离相等,为CA=1.…9分
又AB∥A1B1,∴△MAB的面积S△ABM=
AB•AA1=
…11分
∴VD-MAB=
S△ABM•CA=
•
•AC=
.…12分.
∴∠A1MD或其补角是异面直线DM与AB所成的角.…3分
连接A1D,则三角形A1DM为直角三角形,且∠DA1M=900,A1D=
| ||
| 2 |
| 1 |
| 2 |
∴tan∠A1MD=
| A1D |
| A1M |
| 5 |
∴异面直线DM与AB所成的角为arctan
| 5 |
(2)CC1∥平面AA1B1B即CC1∥平面MAB(不必证明)…7分
∵CA⊥AB,CA⊥AA1,AB∩AA1=A,
∴CA⊥平面AA1B1B
∴C到平面AA1B1B的距离为CA=1.
∵CC1∥平面AA1B1B,
可知D到平面AA1B1B的距离与C到平面AA1B1B的距离相等,为CA=1.…9分
又AB∥A1B1,∴△MAB的面积S△ABM=
| 1 |
| 2 |
| 1 |
| 2 |
∴VD-MAB=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题考查异面直线及其所成的角,考查体积的计算,考查学生分析解决问题的能力,难度中等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x),g(x)都是定义在R上的函数,且满足以下条件:
①f(x)为奇函数,g(x)为偶函数;
②f(1)=0,g(x)≠0;
③当x>0时,总有f(x)•g′(x)<f′(x)•g(x).
则
>0的解集为( )
①f(x)为奇函数,g(x)为偶函数;
②f(1)=0,g(x)≠0;
③当x>0时,总有f(x)•g′(x)<f′(x)•g(x).
则
| f(x-2) |
| g(x-2) |
| A、(1,2)∪(3,+∞) |
| B、(-1,0)∪(1,+∞) |
| C、(-3,-2)∪(-1,+∞) |
| D、(-1,0)∪(3,+∞) |
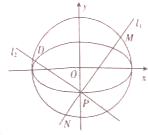 已知椭圆E:
已知椭圆E: