题目内容
在平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠BCD=135°,沿对角线AC将四边形折成直二面角,如图所示:

(Ⅰ)求证:AB⊥平面BCD;
(Ⅱ)求二面角B-AD-C的平面角的余弦值.

(Ⅰ)求证:AB⊥平面BCD;
(Ⅱ)求二面角B-AD-C的平面角的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(I)由平面几何知识,不难算出∠ACD=90°,从而AC⊥CD.因为二面角B-AC-D为直二面角,结合CD⊥AC,可得DC⊥平面ABC,得到CD⊥AB,最后根据线面垂直的判定定理,得到AB⊥平面BCD;
(II)设AC的中点为O,连接BO,过O作OE⊥AD于E,可证∠BEO为二面角B-AD-C的平面角,解直角三角形BEO,可求此角的大小,即可得出结论.
(II)设AC的中点为O,连接BO,过O作OE⊥AD于E,可证∠BEO为二面角B-AD-C的平面角,解直角三角形BEO,可求此角的大小,即可得出结论.
解答:
 (I)证明:∵∠B=90°,∴AB⊥BC.
(I)证明:∵∠B=90°,∴AB⊥BC.
∵AB=BC,∴∠BCA=∠BAC=45°.(1分)
又平面四边形ABCD中,∠C=135°,
∴∠DCA=90°∴DC⊥AC(2分)
∵平面ABC⊥平面ACD,平面ABC∩平面ACD=AC,DC?平面ACD,
∴DC⊥平面ABC,∴AB⊥CD(4分)
∵DC∩BC=C,∴AB⊥平面BCD(5分)
∵AB?平面ABD,∴平面ABD⊥平面PCD.(6分)
(II)解:设AC的中点为O,连接BO,过O作OE⊥AD于E,连接BE.
∵AB=BC,O为AC中点.∴BO⊥AC,(7分)
∵平面ABC⊥平面ACD,平面ABC∩平面ACD=AC,
BO?平面ABC,∴BO⊥平面ACD.(8分)
∵OE⊥AD,
∴BE⊥AD,∴∠BEO为二面角B-AD-C的平面角.(10分)
在Rt△ABC中,BO=
,AC=
∴在Rt△DCA中,AD=
,∴OE=
.(11分)
∴在Rt△BOE中,tan∠BEO=
=
,∴∠BEO=60°(13分)
∴二面角B-AD-C的大小为60°,
∴其余弦值为
(14分)
 (I)证明:∵∠B=90°,∴AB⊥BC.
(I)证明:∵∠B=90°,∴AB⊥BC.∵AB=BC,∴∠BCA=∠BAC=45°.(1分)
又平面四边形ABCD中,∠C=135°,
∴∠DCA=90°∴DC⊥AC(2分)
∵平面ABC⊥平面ACD,平面ABC∩平面ACD=AC,DC?平面ACD,
∴DC⊥平面ABC,∴AB⊥CD(4分)
∵DC∩BC=C,∴AB⊥平面BCD(5分)
∵AB?平面ABD,∴平面ABD⊥平面PCD.(6分)
(II)解:设AC的中点为O,连接BO,过O作OE⊥AD于E,连接BE.
∵AB=BC,O为AC中点.∴BO⊥AC,(7分)
∵平面ABC⊥平面ACD,平面ABC∩平面ACD=AC,
BO?平面ABC,∴BO⊥平面ACD.(8分)
∵OE⊥AD,
∴BE⊥AD,∴∠BEO为二面角B-AD-C的平面角.(10分)
在Rt△ABC中,BO=
| ||
| 2 |
| 2 |
∴在Rt△DCA中,AD=
| 3 |
| ||
| 6 |
∴在Rt△BOE中,tan∠BEO=
| BO |
| OE |
| 3 |
∴二面角B-AD-C的大小为60°,
∴其余弦值为
| 1 |
| 2 |
点评:证明两个平面垂直,关键在一个面内找到一条直线和另一个平面垂直,利用三垂线定理找出二面角的平面角,解三角形求出此角

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=2x2+bx+c(b,c∈R)的值域为[0,+∞),若关于x的不等式f(x)<m的解集为(n,n+10),则实数m的值为( )
| A、25 | B、-25 |
| C、50 | D、-50 |

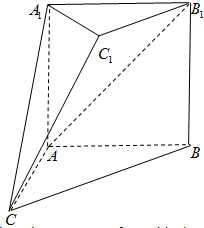 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,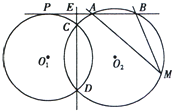 已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1,∠AMB=30°,求⊙O2的半径.
已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1,∠AMB=30°,求⊙O2的半径.