题目内容
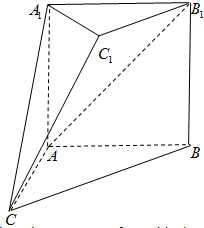 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=| 2 |
| 1 |
| 2 |
(1)求证:A1B1⊥平面AA1C;
(2)求证:AB1∥平面A1C1C.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)根据勾股定理的逆定理,可得AB⊥AC,又因为四边形A1ABB1是正方形,所以AB⊥AA1,从而得到AB⊥平面AA1C,再证AB∥A1B1,可得A1B1⊥平面AA1C;
(2)取BC中点D,连接AD,B1D,C1D.证明四边形B1C1DB是平行四边形,可得C1D∥B1B,进而可证AD∥平面A1C1C;同理,B1D∥平面A1C1C,利用面面平行的判定,可得平面ADB 1∥平面A1C1C,从而可得AB1∥平面A1C1C
(2)取BC中点D,连接AD,B1D,C1D.证明四边形B1C1DB是平行四边形,可得C1D∥B1B,进而可证AD∥平面A1C1C;同理,B1D∥平面A1C1C,利用面面平行的判定,可得平面ADB 1∥平面A1C1C,从而可得AB1∥平面A1C1C
解答:
 证明:(1)因为AB=AC,BC=
证明:(1)因为AB=AC,BC=
AB
所以AB2+AC2=BC2,所以AB⊥AC.
又因为四边形A1ABB1是正方形,所以AB⊥AA1.
又因为AA1∩AC=A,所以AB⊥平面AA1C.
因为四边形A1ABB1是正方形,所以AB∥A1B1,
所以A1B1⊥平面AA1C
(2)取BC的中点D,连接AD,B1D,C1D
因为B1C1∥BC且B1C1=
BC
所以B1C1DB是平行四边形,故C1D1∥B1B,且C1D1=B1B
又A1A∥B1B且A1A=B1B,所以A1A∥C1D,且A1A=C1D
所以A1ADC1是平行四边形
所以A1C1∥AD,所以AD∥平面A1C1C
同理B1D∥平面A1C1C
又因为B1D∩AD=D,所以平面ADB1∥平面A1C1C
所以AB1∥平面A1C1C
 证明:(1)因为AB=AC,BC=
证明:(1)因为AB=AC,BC=| 2 |
所以AB2+AC2=BC2,所以AB⊥AC.
又因为四边形A1ABB1是正方形,所以AB⊥AA1.
又因为AA1∩AC=A,所以AB⊥平面AA1C.
因为四边形A1ABB1是正方形,所以AB∥A1B1,
所以A1B1⊥平面AA1C
(2)取BC的中点D,连接AD,B1D,C1D
因为B1C1∥BC且B1C1=
| 1 |
| 2 |
所以B1C1DB是平行四边形,故C1D1∥B1B,且C1D1=B1B
又A1A∥B1B且A1A=B1B,所以A1A∥C1D,且A1A=C1D
所以A1ADC1是平行四边形
所以A1C1∥AD,所以AD∥平面A1C1C
同理B1D∥平面A1C1C
又因为B1D∩AD=D,所以平面ADB1∥平面A1C1C
所以AB1∥平面A1C1C
点评:本题考查线面平行、线面垂直,掌握线面平行、线面垂直的判定方法是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
定义
?
=
,若
=(1,2),
=(3,-2),则与
?
反向的向量为( )
| a |
| b |
| ||||
|
| a |
| b |
| a |
| b |
| A、(5,-6) |
| B、(5,6) |
| C、(-5,6) |
| D、(-5,-6) |
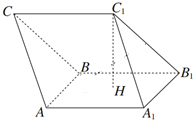 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2
 如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:CE2=EF•EA.
如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:CE2=EF•EA.