题目内容
在直线x-y+4=0上求一点P,使点P到点M(-2,-4),N(4,6)的距离相等.
考点:点到直线的距离公式
专题:直线与圆
分析:设直线x-y+4=0上的一点P(x,x+4),由P到点M(-2,-4),N(4,6)的距离相等,求出点P的坐标.
解答:
解:设在直线x-y+4=0上取一点P(x,x+4),
则点P到点M(-2,-4),N(4,6)的距离为
|PM|=|PN|,
即
=
,
两边平方,得(x+2)2+(x+8)2=(x-4)2+(x-2)2,
解得x=-1.5,
∴y=-1.5+4=2.5;
∴点P为(-1.5,2.5).
则点P到点M(-2,-4),N(4,6)的距离为
|PM|=|PN|,
即
| (x+2)2+(x+4+4)2 |
| (x-4)2+(x+4-6)2 |
两边平方,得(x+2)2+(x+8)2=(x-4)2+(x-2)2,
解得x=-1.5,
∴y=-1.5+4=2.5;
∴点P为(-1.5,2.5).
点评:本题考查了直线方程的应用问题,解题时应用两点间的距离进行解答,是基础题.

练习册系列答案
相关题目
| log89 |
| log23 |
| A、1 | ||
| B、0 | ||
| C、-1 | ||
D、
|
设集合M={x|x+1>0},N={x|x-2<0},则M∩N=( )
| A、(-1,+∞) |
| B、[-1,2) |
| C、(-1,2) |
| D、[-1,2] |
如图所示是四棱锥的三视图,则该几何的体积等于( )
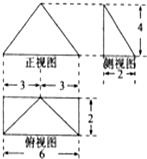

| A、16 | ||
B、34+6
| ||
| C、6 | ||
D、17+6
|