题目内容
 设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图,则不等式f(x)≤0的解集为
设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图,则不等式f(x)≤0的解集为考点:奇偶函数图象的对称性
专题:函数的性质及应用
分析:根据奇函数关于原点对称的性质即可得到结论.
解答:
解:由图象可知:当x>0时,f(x)≤0解得2≤x≤5,f(x)≥0解得0≤x≤2;
当x<0时,-x>0,
因为f(x)为奇函数,
所以f(x)≤0,
即-f(-x)≤0⇒f(-x)≥0⇒0≤-x≤2,
解得-2≤x≤0.
综上,不等式f(x)≤0的解集为{x|-2≤x≤0,或2≤x≤5}.
故答案为:[-2,0]∪[2,5].
当x<0时,-x>0,
因为f(x)为奇函数,
所以f(x)≤0,
即-f(-x)≤0⇒f(-x)≥0⇒0≤-x≤2,
解得-2≤x≤0.
综上,不等式f(x)≤0的解集为{x|-2≤x≤0,或2≤x≤5}.
故答案为:[-2,0]∪[2,5].
点评:本题主要考查不等式的求解,根据奇函数的对称性是解决本题的关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
复数
在复平面上对应的点位于( )
| i |
| 3-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
下列函数为幂函数的是( )
①y=x2+1; ②y=2x; ③y=
; ④y=(x-1)2; ⑤y=x5; ⑥y=xx+1.
①y=x2+1; ②y=2x; ③y=
| 1 |
| x2 |
| A、①③⑤ | B、①②⑤ |
| C、③⑤ | D、④⑤⑥ |
| log89 |
| log23 |
| A、1 | ||
| B、0 | ||
| C、-1 | ||
D、
|
“a>b”是“log2a>log2b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
如图所示是四棱锥的三视图,则该几何的体积等于( )
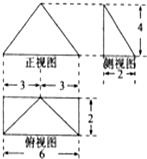

| A、16 | ||
B、34+6
| ||
| C、6 | ||
D、17+6
|

 如图所示,曲线是幂函数y=xa在第一象限内的图象,已知α分别取-1,1,
如图所示,曲线是幂函数y=xa在第一象限内的图象,已知α分别取-1,1,