题目内容
已知函数f(x)=1-
(a>0,a≠1)且f(0)=0.
(Ⅰ)求a的值;
(Ⅱ)若函数g(x)=(2x+1)•f(x)+k有零点,求实数k的取值范围.
(Ⅲ)当x∈(0,1)时,f(x)>m•2x-2恒成立,求实数m的取值范围.
| 4 |
| 2ax+a |
(Ⅰ)求a的值;
(Ⅱ)若函数g(x)=(2x+1)•f(x)+k有零点,求实数k的取值范围.
(Ⅲ)当x∈(0,1)时,f(x)>m•2x-2恒成立,求实数m的取值范围.
考点:指数函数综合题
专题:函数的性质及应用
分析:(Ⅰ)由函数f(x)的解析式以及f(0)=1-
=0,求得a的值.
(Ⅱ)由题意可得,函数y=2x 的图象和直线y=1-k有交点,故有1-k>0,求得k的范围.
(Ⅲ)由题意可得当x∈(0,1)时,1-
>m•2x-2恒成立.令t=2x,则t∈(1,2),且 m<
+
.利用单调性求得
+
>
,从而可得m的范围.
| 4 |
| 2+a |
(Ⅱ)由题意可得,函数y=2x 的图象和直线y=1-k有交点,故有1-k>0,求得k的范围.
(Ⅲ)由题意可得当x∈(0,1)时,1-
| 2 |
| 2x+1 |
| 1 |
| t |
| 2 |
| t+1 |
| 1 |
| t |
| 2 |
| t+1 |
| 7 |
| 6 |
解答:
解:(Ⅰ)对于函数f(x)=1-
(a>0,a≠1),由f(0)=1-
=0,
求得a=2,故f(x)=1-
=1-
.
(Ⅱ)若函数g(x)=(2x+1)•f(x)+k=2x+1-2+k=2x-1+k 有零点,
则函数y=2x 的图象和直线y=1-k有交点,∴1-k>0,求得k<1.
(Ⅲ)∵当x∈(0,1)时,f(x)>m•2x-2恒成立,即1-
>m•2x-2恒成立.
令t=2x,则t∈(1,2),且 m<
-
=
=
+
.
由于
+
在∈(1,2)上单调递减,∴
+
>
+
=
,∴m≤
.
| 4 |
| 2ax+a |
| 4 |
| 2+a |
求得a=2,故f(x)=1-
| 4 |
| 2•2x+2 |
| 2 |
| 2x+1 |
(Ⅱ)若函数g(x)=(2x+1)•f(x)+k=2x+1-2+k=2x-1+k 有零点,
则函数y=2x 的图象和直线y=1-k有交点,∴1-k>0,求得k<1.
(Ⅲ)∵当x∈(0,1)时,f(x)>m•2x-2恒成立,即1-
| 2 |
| 2x+1 |
令t=2x,则t∈(1,2),且 m<
| 3 |
| t |
| 2 |
| t(t+1) |
| 3t+1 |
| t(t+1) |
| 1 |
| t |
| 2 |
| t+1 |
由于
| 1 |
| t |
| 2 |
| t+1 |
| 1 |
| t |
| 2 |
| t+1 |
| 1 |
| 2 |
| 2 |
| 2+1 |
| 7 |
| 6 |
| 7 |
| 6 |
点评:本题主要考查指数函数的性质综合应用,函数的恒成立问题,体现了转化的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
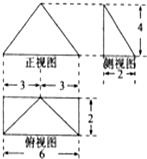
如图所示是四棱锥的三视图,则该几何的体积等于( )

| A、16 | ||
B、34+6
| ||
| C、6 | ||
D、17+6
|
设集合P={3,log2a},Q={a,b},若P∩Q={0},则P∪Q=( )
| A、{3,0} |
| B、{3,1,0} |
| C、{3,2,0} |
| D、{3,2,1,0} |
一个几何体的三视图如图所示,则这个几何体的体积为( )


| A、6.5 | B、7 | C、7.5 | D、8 |