题目内容
1.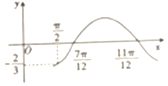 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的 部分图象如图所示,f($\frac{π}{2}$)=-$\frac{2}{3}$,则f($\frac{π}{3}$)等于( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的 部分图象如图所示,f($\frac{π}{2}$)=-$\frac{2}{3}$,则f($\frac{π}{3}$)等于( )| A. | -$\frac{2}{3}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{2}}{4}$ | D. | $\frac{1}{4}$ |
分析 首先由函数图象求出解析式然后求三角函数值.
解答 解:由图象得到函数周期为T=2($\frac{11π}{12}-\frac{7π}{12}$)=$\frac{2}{3}$π=$\frac{2π}{ω}$,所以ω=3,由f($\frac{7π}{12}$)=0得到φ=$\frac{π}{4}$,
由f($\frac{π}{2}$)=-$\frac{2}{3}$,得到Asin($\frac{3π}{2}+\frac{π}{4}$)=$-\frac{2}{3}$,所以A=$\frac{2\sqrt{2}}{3}$,
所以f(x)=$\frac{2\sqrt{2}}{3}$sin(3x+$\frac{π}{4}$),所以f($\frac{π}{3}$)=$\frac{2\sqrt{2}}{3}sin(3×\frac{π}{3}+\frac{π}{4})$=$-\frac{2}{3}$;
故选:A.
点评 本题考查了三角函数图象以及性质;熟练掌握正弦函数的图象和性质是解答的关键.

练习册系列答案
相关题目
11.已知函数f(x)=4ex(x+1)-k($\frac{2}{3}$x3+2x2),若x=-2是函数f(x)的唯一一个极值点,则实数k的取值范围是( )
| A. | (-2e,e] | B. | [0,2e] | C. | (-∞,-e)∪[e,2e] | D. | (-∞,-e)∪[0,e] |
9.若函数f(x)=$\frac{1}{2}$x2+2x-3lnx+4a的极小值为-$\frac{3}{2}$,则a的值为( )
| A. | -2 | B. | -1 | C. | -4 | D. | -3 |
13.已知函数f(x)=$\left\{\begin{array}{l}{g(x),x<0}\\{a-lo{g}_{2}(x+2),x≥0}\end{array}\right.$是奇函数,则f(x)>-1的解集为( )
| A. | (-2,0]∪(2,+∞) | B. | (-2,+∞) | C. | (-∞,-2)∪(0,2) | D. | (-∞,2) |
10.下列命题中,正确的是( )
①?x∈R,2x>3x;②“x≠3”是“|x|≠3”成立的充分条件;③空间中若直线l若平行于平面α,则α内所有直线均与l是异面直线;④空间中有三个角是直角的四边形不一定是平面图形.
①?x∈R,2x>3x;②“x≠3”是“|x|≠3”成立的充分条件;③空间中若直线l若平行于平面α,则α内所有直线均与l是异面直线;④空间中有三个角是直角的四边形不一定是平面图形.
| A. | ①③ | B. | ①④ | C. | ②④ | D. | ②③ |
11. 如图,已知A、B分别是函数f(x)=$\sqrt{3}$cos(ωx-$\frac{π}{2}$)(ω>0)在y轴右侧图象上的第一个最高点和第一个最低点,且∠AOB=$\frac{π}{2}$,则为了得到函数y=$\sqrt{3}$sin($\frac{π}{2}$x+$\frac{π}{3}$)的图象,只需把函数y=f(x)的图象( )
如图,已知A、B分别是函数f(x)=$\sqrt{3}$cos(ωx-$\frac{π}{2}$)(ω>0)在y轴右侧图象上的第一个最高点和第一个最低点,且∠AOB=$\frac{π}{2}$,则为了得到函数y=$\sqrt{3}$sin($\frac{π}{2}$x+$\frac{π}{3}$)的图象,只需把函数y=f(x)的图象( )
 如图,已知A、B分别是函数f(x)=$\sqrt{3}$cos(ωx-$\frac{π}{2}$)(ω>0)在y轴右侧图象上的第一个最高点和第一个最低点,且∠AOB=$\frac{π}{2}$,则为了得到函数y=$\sqrt{3}$sin($\frac{π}{2}$x+$\frac{π}{3}$)的图象,只需把函数y=f(x)的图象( )
如图,已知A、B分别是函数f(x)=$\sqrt{3}$cos(ωx-$\frac{π}{2}$)(ω>0)在y轴右侧图象上的第一个最高点和第一个最低点,且∠AOB=$\frac{π}{2}$,则为了得到函数y=$\sqrt{3}$sin($\frac{π}{2}$x+$\frac{π}{3}$)的图象,只需把函数y=f(x)的图象( )| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向左平行移动$\frac{1}{3}$个单位长度 | ||
| C. | 向左平行移动$\frac{2}{3}$个单位长度 | D. | 向左平行移动$\frac{2π}{3}$个单位长度 |