题目内容
16．已知函数f（x）=（2x-1）2+5x（1）求f′（x）
（2）求曲线y=f（x）在点（2，19）处的切线方程．
分析 （1）根据求导公式求出f（x）的导数即可；
（2）求出切线的斜率f′（2），从而求出切线方程即可．
解答 解：（1）f′（x）=4（2x-1）+5=8x+1；
（2）f′（2）=17，
故切线方程是：y-19=17（x-2），
即17x-y-15=0．
点评 本题考查了求导问题，考查求切线方程问题，是一道基础题．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
6．设集合A={x|log2（x+1）＜2}，B={y|y=$\sqrt{16-{2}^{x}}$}，则（∁RA）∩B=（ ）
| A． | （0，3） | B． | [0，4] | C． | [3，4） | D． | （-1，3） |
7．为了解某种产品的月广告费用x（单位：万元）对月销售量y（单位：万台）的影响，收集到如下5个月的统计数据：
根据上表中的数据可得线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其中$\stackrel{∧}{b}$=4.2，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，据此估计，该产品的月广告费为13万元时的月销售量为（ ）
| 广告费x（万元） | 1 | 2 | 3 | 4 | 5 |
| 销售量y（万台） | 2 | 5 | 10 | 15 | 18 |
| A． | 30 | B． | 52 | C． | 57.2 | D． | 70 |
4．A${\;}_{5}^{2}$-C${\;}_{5}^{3}$等于（ ）
| A． | 0 | B． | -10 | C． | 10 | D． | -40 |
1．
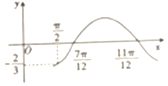已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的 部分图象如图所示，f（$\frac{π}{2}$）=-$\frac{2}{3}$，则f（$\frac{π}{3}$）等于（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的 部分图象如图所示，f（$\frac{π}{2}$）=-$\frac{2}{3}$，则f（$\frac{π}{3}$）等于（ ）| A． | -$\frac{2}{3}$ | B． | -$\frac{1}{2}$ | C． | -$\frac{\sqrt{2}}{4}$ | D． | $\frac{1}{4}$ |
8．设集合A={x|x2-4x+3＜0}，U={x|x-1＞0}，则∁UA=（ ）
| A． | （3，+∞） | B． | [3，+∞） | C． | （1，3） | D． | （1，+∞） |
6．设向量$\overrightarrow{a}$，$\overrightarrow{b}$是互相垂直的两个单位向量，且|$\overrightarrow{a}$-3$\overrightarrow{b}$|=m|$\overrightarrow{a}$+$\overrightarrow{b}$|，则实数m的值为（ ）
| A． | $\sqrt{10}$ | B． | ±$\sqrt{10}$ | C． | $\sqrt{5}$ | D． | ±$\sqrt{5}$ |