��Ŀ����
11�� ��ͼ����֪A��B�ֱ��Ǻ���f��x��=$\sqrt{3}$cos����x-$\frac{��}{2}$�����أ�0����y���Ҳ�ͼ���ϵĵ�һ����ߵ�͵�һ����͵㣬�ҡ�AOB=$\frac{��}{2}$����Ϊ�˵õ�����y=$\sqrt{3}$sin��$\frac{��}{2}$x+$\frac{��}{3}$����ͼ��ֻ��Ѻ���y=f��x����ͼ������
��ͼ����֪A��B�ֱ��Ǻ���f��x��=$\sqrt{3}$cos����x-$\frac{��}{2}$�����أ�0����y���Ҳ�ͼ���ϵĵ�һ����ߵ�͵�һ����͵㣬�ҡ�AOB=$\frac{��}{2}$����Ϊ�˵õ�����y=$\sqrt{3}$sin��$\frac{��}{2}$x+$\frac{��}{3}$����ͼ��ֻ��Ѻ���y=f��x����ͼ������| A�� | ����ƽ���ƶ�$\frac{��}{3}$����λ���� | B�� | ����ƽ���ƶ�$\frac{1}{3}$����λ���� | ||
| C�� | ����ƽ���ƶ�$\frac{2}{3}$����λ���� | D�� | ����ƽ���ƶ�$\frac{2��}{3}$����λ���� |
���� �����A��B�����꣬����������������ֱ�����ʣ�������������������ʽ���T��ֵ���ɵæص�ֵ�������ú���y=Asin����x+�գ���ͼ��任���ɣ��ij����ۣ�
��� �⣺����f��x��=$\sqrt{3}$cos����x-$\frac{��}{2}$��=$\sqrt{3}$sin��x���躯��f��x��������ΪT�����A��$\frac{T}{4}$��$\sqrt{3}$����B��$\frac{3T}{4}$��-$\sqrt{3}$����
���ݡ�AOB=$\frac{��}{2}$���ɵ�$\overrightarrow{OA}•\overrightarrow{OB}$=$\frac{{3T}^{2}}{16}$-3=0����T=4=$\frac{2��}{��}$�����=$\frac{��}{2}$��f��x��=$\sqrt{3}$sin$\frac{��}{2}$x��
���ں���y=$\sqrt{3}$sin��$\frac{��}{2}$x+$\frac{��}{3}$��=$\sqrt{3}$sin$\frac{��}{2}$��x+$\frac{2}{3}$����
��ֻ��Ѻ���y=f��x����ͼ������ƽ���ƶ�$\frac{2}{3}$����λ���ȣ�
��ѡ��C��
���� ��������Ҫ�����յ���ʽ�����Һ����������ԣ�����������ֱ�����ʣ�������������������ʽ������y=Asin����x+�գ���ͼ��任���ɣ����ڻ����⣮

 ��У����ϵ�д�
��У����ϵ�д�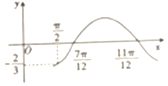 ��֪����f��x��=Asin����x+�գ���A��0���أ�0��0���գ�$\frac{��}{2}$���� ����ͼ����ͼ��ʾ��f��$\frac{��}{2}$��=-$\frac{2}{3}$����f��$\frac{��}{3}$�����ڣ�������
��֪����f��x��=Asin����x+�գ���A��0���أ�0��0���գ�$\frac{��}{2}$���� ����ͼ����ͼ��ʾ��f��$\frac{��}{2}$��=-$\frac{2}{3}$����f��$\frac{��}{3}$�����ڣ�������| A�� | -$\frac{2}{3}$ | B�� | -$\frac{1}{2}$ | C�� | -$\frac{\sqrt{2}}{4}$ | D�� | $\frac{1}{4}$ |
| A�� | $\frac{1-ln2}{2}$ | B�� | $\frac{3-2ln2}{4}$ | C�� | $\frac{1+ln2}{2}$ | D�� | $\frac{1+2ln2}{2}$ |
| A�� | $\sqrt{10}$ | B�� | ��$\sqrt{10}$ | C�� | $\sqrt{5}$ | D�� | ��$\sqrt{5}$ |
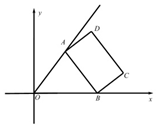 ��֪����OP��y=$\frac{4}{3}$x��x��0���;���ABCD��AB=16��AD=9����A��B�ֱ�������OP��x��Ǹ������ϣ����߶�OD���ȵ����ֵΪ��������
��֪����OP��y=$\frac{4}{3}$x��x��0���;���ABCD��AB=16��AD=9����A��B�ֱ�������OP��x��Ǹ������ϣ����߶�OD���ȵ����ֵΪ��������| A�� | $\sqrt{337}$ | B�� | 27 | C�� | $\sqrt{689}$ | D�� | 29 |
 ��ͼ���ı���ABCD�������Σ��ı���ABEG��ƽ���ı��Σ���ƽ��ABCD��ƽ��ABEG��AE��AB��EF��AG��F�����߶�CD��AE���е�ֱ�ΪP��M��
��ͼ���ı���ABCD�������Σ��ı���ABEG��ƽ���ı��Σ���ƽ��ABCD��ƽ��ABEG��AE��AB��EF��AG��F�����߶�CD��AE���е�ֱ�ΪP��M��