题目内容
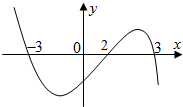 若连续函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
若连续函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A、f(x)有极大值f(3)和极小值f(2) |
| B、f(x)有极大值f(-3)和极小值f(2) |
| C、f(x)有极大值f(3)和极小值f(-3) |
| D、f(x)有极大值f(-3)和极小值f(3) |
考点:利用导数研究函数的极值
专题:导数的概念及应用
分析:先判断出各个区间上的导数的符号,再判断出函数的单调区间,从而求出极值.
解答:
解:①x<-3时,2-x>0,y>0,∴f′(x)>0,
②-3<x<2时,2-x>0,y<0,∴f′(x)<0,
③2<x<3时,2-x<0,y>0,∴f′(x)<0,
④x>3时,2-x<0,y<0,∴f′(x)>0,
∴f(x)在(-∞,-3),(3,+∞)上递增,在(-3,3)递减,
∴f(3)是极小值,f(-3)是极大值;
故选:D.
②-3<x<2时,2-x>0,y<0,∴f′(x)<0,
③2<x<3时,2-x<0,y>0,∴f′(x)<0,
④x>3时,2-x<0,y<0,∴f′(x)>0,
∴f(x)在(-∞,-3),(3,+∞)上递增,在(-3,3)递减,
∴f(3)是极小值,f(-3)是极大值;
故选:D.
点评:本题考察了函数的单调性,求函数的极值问题,是一道基础题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
下列函数中增加得最快的是( )
| A、y=2x |
| B、y=3x |
| C、y=4x |
| D、y=ex |
根据下列情况,判断三角形解的情况,其中正确的是( )
| A、a=8,b=16,A=30°,有两解 |
| B、b=18,c=20,B=60°,有一解 |
| C、a=5,c=2,A=90°,无解 |
| D、a=30,b=25,A=150°,有一解 |
一个算法的程序框图如图,则其输出结果是( )
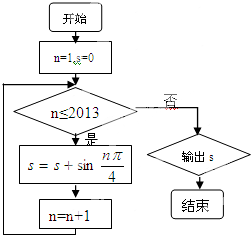

| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,内角A、B、C的对边分别是a、b、c,若b2-c2=
ac,sinA=2
sinC,则B=( )
| 3 |
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
已知F1,F2分别为双曲线
-
=1(a>0,b>0)的左、右焦点,O为原点,A为右顶点,P为双曲线左支上的任意一点,若
存在最小值为12a,则双曲线离心率e的取值范围是 ( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1|-|OA| |
| A、[5,+∞) |
| B、(2,5] |
| C、(1,5] |
| D、(1,2) |
在△ABC中,角A=30°,B=60°,则b:c=( )
| A、1:2 | ||
| B、2:3 | ||
C、1:
| ||
D、
|