题目内容
数列1，
，
，
，
，
，…，
，
，…，
…的前18项的和（ ）
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| n |
| 2 |
| n |
| n |
| n |
| A、11 | ||
B、
| ||
C、
| ||
| D、10 |
考点：数列的求和
专题：等差数列与等比数列
分析：由S18=1+（
+
）+（
+
+
）+（
+
+
+
）+（
+
+
+
+
）+（
+
+
），能求出结果．
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| 4 |
| 2 |
| 4 |
| 3 |
| 4 |
| 4 |
| 4 |
| 1 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 5 |
| 5 |
| 1 |
| 6 |
| 2 |
| 6 |
| 3 |
| 6 |
解答：
解：数列1，
，
，
，
，
，…，
，
，…，
…的前18项的和：
S18=1+（
+
）+（
+
+
）+（
+
+
+
）+（
+
+
+
+
）+（
+
+
）
=1+
+2+
+3+1
=11．
故选：A．
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| n |
| 2 |
| n |
| n |
| n |
S18=1+（
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| 4 |
| 2 |
| 4 |
| 3 |
| 4 |
| 4 |
| 4 |
| 1 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 5 |
| 5 |
| 1 |
| 6 |
| 2 |
| 6 |
| 3 |
| 6 |
=1+
| 3 |
| 2 |
| 5 |
| 2 |
=11．
故选：A．
点评：本题考查数列的前n项和的求法，是基础题，解题时要认真审题．
练习册系列答案
阅读快车系列答案
相关题目
在△ABC中，三条边长分别为4cm，5cm，7cm，则此三角形的形状是（ ）
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、不能确定 |
已知a≥4，x＞0，y＞0，则（ax+y）（
+
）的最小值是（ ）
| 1 |
| x |
| 1 |
| y |
| A、6 | B、7 | C、8 | D、9 |
向量
=（-2，-1），
=（λ，1），若
与
夹角为钝角，则λ取值范围是（ ）
| a |
| b |
| a |
| b |
A、（-
| ||
| B、（2，+∞） | ||
C、（-
| ||
D、（-∞，-
|
已知双曲线my2-x2=1（m∈R）与椭圆
+x2=1有相同的焦点，则该双曲线的渐近线方程为（ ）
| y2 |
| 5 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
| D、y=±3x |
不同三点A，B，C满足（
•
）：（
•
）：（
•
）=3：4：5，则这三点（ ）
| BC |
| CA |
| CA |
| AB |
| AB |
| BC |
| A、组成锐角三角形 |
| B、组成直角三角形 |
| C、组成钝角三角形 |
| D、在同一条直线上 |
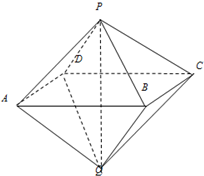如图，已知两个正四棱锥P-ABCD与Q-ABCD的高都是2，AB=4． 
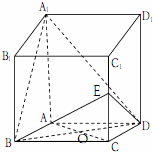四棱柱ABCD-A1B1C1D1中，AA1⊥底面ABCD，且ABCD是菱形，AB=BC=2，AA1=4，∠ABC=60°．