题目内容
不同三点A，B，C满足（
•
）：（
•
）：（
•
）=3：4：5，则这三点（ ）
| BC |
| CA |
| CA |
| AB |
| AB |
| BC |
| A、组成锐角三角形 |
| B、组成直角三角形 |
| C、组成钝角三角形 |
| D、在同一条直线上 |
考点：平面向量数量积的运算
专题：解三角形,平面向量及应用
分析：由条件可设三组数量积分别为，3m，4m，5m，然后观察三组数量积会发现，每两组数量积里都有相同的向量，对每两组数量积相加看出现什么情况，要判断三点共线，还是构成三角形，一般要看边的关系，若得出边的关系，本题答案可能就找到了．
解答：
解：由题意设：
•
=3m，
•
=4m，
•
=5m，（m≠0）；
•
+
•
=
(
+
)=
•
=-(
)2=7m；
•
+
•
=
(
+
)=-(
)2=9m；
•
+
•
=-(
)2=8m；所以，|
|2=-7m，|
|2=-9m，|
|2=-8m
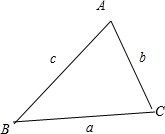
显然，不存在两边之和等于第三遍的情况，故三点不在一条直线上，所以三点构成三角形，如下图，设A，B，C三点所对三边长分别为a，b，c，则由余弦定理得：cos∠ ACB=
=-
＞0，所以∠C是锐角，又∠C是最大边所对角，所以∠C最大，所以△ABC是锐角三角形．故答案选A．
| BC |
| CA |
| CA |
| AB |
| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
| CA |
| BC |
| AB |
| CA |
| AC |
| CA |
| CA |
| AB |
| AB |
| BC |
| AB |
| CA |
| BC |
| AB |
| AB |
| BC |
| BC |
| CA |
| BC |
| CA |
| AB |
| BC |
显然，不存在两边之和等于第三遍的情况，故三点不在一条直线上，所以三点构成三角形，如下图，设A，B，C三点所对三边长分别为a，b，c，则由余弦定理得：cos∠ ACB=
| a2+b2-c2 |
| 2ab |
| 32m | ||||
|
点评：由比值的情况设出三组数量积的值，是解本题的关键，然后表示出了三边长度的平方，也就表示出了三边长度．而判断三点是否共线，只需说明两边之和是否等于第三边；而要判断是什么三角形，只需求出大边对的角的余弦值是大于0，等于0，还是小于0即可，这时需要应用余弦定理．
练习册系列答案
名校课堂系列答案
相关题目
对于曲线y=ae
，令μ=lny，c=lna，v=
，可变换为线性回归模型，其形式为（ ）
| b |
| x |
| 1 |
| x |
| A、y=a+bv |
| B、μ=a+bv |
| C、μ=c+bv |
| D、y=c+bx |
已知双曲线C：
-
=1（a＞0，b＞0）的一条渐近方程为y=
x，则C的离心率为（ ）
| y2 |
| a2 |
| x2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列1，
，
，
，
，
，…，
，
，…，
…的前18项的和（ ）
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| n |
| 2 |
| n |
| n |
| n |
| A、11 | ||
B、
| ||
C、
| ||
| D、10 |
已知定义在R上的函数f（x），对任意x∈R，都有f（x+2）=-f（x）+f（1）成立，若函数y=f（x+1）的图象关于点（-1，0）对称，则f（2014）=（ ）
| A、3 | B、2014 |
| C、0 | D、-2014 |
若A={x|-1＜x＜2}，B={x|1＜x＜3}，则A∩B=（ ）
| A、{x|1＜x＜2} |
| B、{x|-1＜x＜3} |
| C、{x|1＜x＜3} |
| D、{x|-1＜x＜2} |
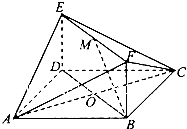如图，已知正方形ABCD和矩形BDFE所在的平面互相垂直，AC交BD于O点，M为EF的中点，BC=