题目内容
向量
=（-2，-1），
=（λ，1），若
与
夹角为钝角，则λ取值范围是（ ）
| a |
| b |
| a |
| b |
A、（-
| ||
| B、（2，+∞） | ||
C、（-
| ||
D、（-∞，-
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由于
与
夹角为钝角，可知
•
=-2λ-1＜0，且
与
夹角不为平角，解出即可．
| a |
| b |
| a |
| b |
| a |
| b |
解答：
解：∵
与
夹角为钝角，∴
•
=-2λ-1＜0，解得λ＞-
，
当λ=2时，
与
夹角为平角，不符合题意．
因此（-
，2）∪（2，+∞）．
故选：A．
| a |
| b |
| a |
| b |
| 1 |
| 2 |
当λ=2时，
| a |
| b |
因此（-
| 1 |
| 2 |
故选：A．
点评：本题考查了向量的夹角公式，属于基础题．
练习册系列答案
相关题目
已知i是虚数单位，z=1+i，
为z的共轭复数，则复数
在复平面上对应的点的坐标为（ ）
. |
| z |
| z2 | ||
|
| A、（1，1） |
| B、（-1，-1） |
| C、（-1，1） |
| D、（1，-1） |
已知f（x）=
，则f（5）=（ ）
| x+2 |
| x-6 |
| A、-8 | B、-7 | C、-6 | D、-5 |
如图，不等式x2-y2-4x-2y+3≥0表示的平面区域是（ ）
A、 |
B、 |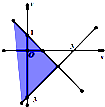
C、 |
D、 |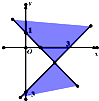
已知双曲线C：
-
=1（a＞0，b＞0）的一条渐近方程为y=
x，则C的离心率为（ ）
| y2 |
| a2 |
| x2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个几何体的三视图及其尺寸，如图所示，则该几何体的侧面积为（ ）
| A、80 | B、40 | C、48 | D、96 |
数列1，
，
，
，
，
，…，
，
，…，
…的前18项的和（ ）
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| n |
| 2 |
| n |
| n |
| n |
| A、11 | ||
B、
| ||
C、
| ||
| D、10 |
若A={x|-1＜x＜2}，B={x|1＜x＜3}，则A∩B=（ ）
| A、{x|1＜x＜2} |
| B、{x|-1＜x＜3} |
| C、{x|1＜x＜3} |
| D、{x|-1＜x＜2} |