题目内容
13.在直角梯形ABCD中,∠A=90°,AD∥BC,BC=2AD,△ABD的面积为2,若$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{EC}$,BE⊥DC,则$\overrightarrow{DA}$$•\overrightarrow{DC}$的值为( )| A. | -2 | B. | -2$\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
分析 如图建立平面直角坐标系,设AD=m,则AD=$\frac{4}{m}$,由BE⊥DC,∴$\overrightarrow{BE}•\overrightarrow{CD}=-\frac{4}{3}{m}^{2}+\frac{8}{3m}×\frac{4}{m}=0$,⇒m即可.
解答 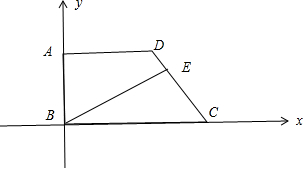 解:如图建立平面直角坐标系,设AD=m,则AD=$\frac{4}{m}$,
解:如图建立平面直角坐标系,设AD=m,则AD=$\frac{4}{m}$,
∴A(0,$\frac{4}{m}$),D(m,$\frac{4}{m}$),C(2m,0)
$\overrightarrow{BC}=(2m,0)$,$\overrightarrow{CD}=(-m,\frac{4}{m})$,$\overrightarrow{BE}=\overrightarrow{BC}+\overrightarrow{CE}=\overrightarrow{BC}+\frac{2}{3}\overrightarrow{CD}$=($\frac{4m}{3},\frac{8}{3m}$)'
∵BE⊥DC,∴$\overrightarrow{BE}•\overrightarrow{CD}=-\frac{4}{3}{m}^{2}+\frac{8}{3m}×\frac{4}{m}=0$,⇒m=$\sqrt{2}$.
∴$\overrightarrow{DA}=(-\sqrt{2},0)$,$\overrightarrow{DC}=(\sqrt{2},-2\sqrt{2})$,
则$\overrightarrow{DA}$$•\overrightarrow{DC}$的值为-$\sqrt{2}$×$\sqrt{2}$+0×$\sqrt{2}$=-2$\sqrt{2}$.
故选:B.
点评 本题考查了,向量的坐标运算,属于基础题.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案| A. | -3 | B. | -4 | C. | -5 | D. | 2 |
| A. | $\frac{5}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{11}{16}$ |
| A. | [-$\frac{1}{4}$,$\frac{1}{4}$) | B. | [-$\frac{1}{4}$,$\frac{1}{4}$] | C. | (-∞,-$\frac{1}{4}$]∪(0,$\frac{1}{4}$) | D. | (-∞,-$\frac{1}{4}$]∪[$\frac{1}{4}$,+∞) |
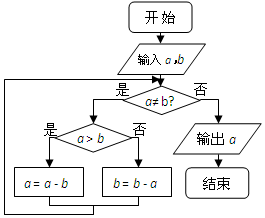 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为225,135,则输出的a=45.
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为225,135,则输出的a=45.