题目内容
18.已知实数a,b满足0<a<1,-1<b<1,则函数y=$\frac{1}{3}$ax3+ax2+b有三个零点的概率为( )| A. | $\frac{5}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{11}{16}$ |
分析 由函数有极值可得b<a2,由定积分可求满足题意的区域面积,由几何概型的概率公式可得.
解答 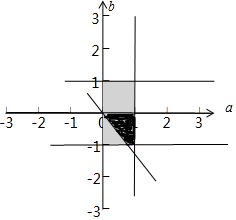 解:对y=$\frac{1}{3}$ax3+ax2+b求导数可得y′=ax2+2ax,令ax2+2ax=0,可得x=0,或x=-2,0<a<1,
解:对y=$\frac{1}{3}$ax3+ax2+b求导数可得y′=ax2+2ax,令ax2+2ax=0,可得x=0,或x=-2,0<a<1,
x=-2是极大值点,x=0是极小值点,函数y=$\frac{1}{3}$ax3+ax2+b有三个零点,可得$\left\{\begin{array}{l}{f(-2)>0}\\{f(0)<0}\end{array}\right.$,即:$\left\{\begin{array}{l}{-\frac{8}{3}a+4a+b=\frac{4}{3}a+b>0}\\{b<0}\end{array}\right.$,
画出可行域如图:满足函数y=$\frac{1}{3}$ax3+ax2+b有三个零点,如图深色区域,实数a,b满足0<a<1,-1<b<1,为长方形区域,所以长方形的面积为:2,实数区域的面积为:$\frac{1}{2}×(1+\frac{1}{4})×1$=$\frac{5}{8}$
∴所求概率为P=$\frac{\frac{5}{8}}{2}$=$\frac{5}{16}$,
故选:A.
点评 本题考查几何概型的求解,涉及导数求解函数的极值,函数的零点以及线性规划的应用,属中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
12.若分别为P(1,0)、Q(2,0),R(4,0)、S(8,0)四个点各作一条直线,所得四条直线恰围成正方形,则该正方形的面积不可能为( )
| A. | $\frac{16}{17}$ | B. | $\frac{36}{5}$ | C. | $\frac{64}{37}$ | D. | $\frac{196}{53}$ |
13.在直角梯形ABCD中,∠A=90°,AD∥BC,BC=2AD,△ABD的面积为2,若$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{EC}$,BE⊥DC,则$\overrightarrow{DA}$$•\overrightarrow{DC}$的值为( )
| A. | -2 | B. | -2$\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
3.已知双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,抛物线C:y2=8ax的焦点为F,若在E的渐近线上存在点P使得PA⊥FP,则E的离心率的取值范围是( )
| A. | (1,2) | B. | (1,$\frac{3\sqrt{2}}{4}$] | C. | (2,+∞) | D. | [$\frac{3\sqrt{2}}{4}$,+∞) |
8.已知函数f(x)=$\left\{\begin{array}{l}{kx+2,x≥0}\\{{(\frac{1}{2})}^{x},x<0}\end{array}\right.$,若方程f(f(x))-$\frac{3}{2}$=0在实数集范围内无解,则实数k的取值范围是( )
| A. | (-1,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,$\frac{1}{3}$) | C. | [0,+∞) | D. | (-$\frac{1}{2}$,-$\frac{1}{4}$] |
 已知三棱柱ABC-A1B1C1的侧棱与底面ABC垂直,且AA1=4,AC=BC=2,∠ACB=90°.
已知三棱柱ABC-A1B1C1的侧棱与底面ABC垂直,且AA1=4,AC=BC=2,∠ACB=90°.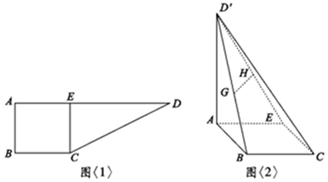 如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,如图<2>:若G,H分别为D′B,D′E的中点.
如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,如图<2>:若G,H分别为D′B,D′E的中点.