题目内容

7．计算∫x2arctanxdx，可设u=arctanx，dv=$\frac{1}{{x}^{2}}$dx．

分析 根据分部积分法即可得到答案．

解答 解：∫x2arctanxdx，可设u=arctanx，dv=$\frac{1}{{x}^{2}}$dx
故答案为：arctanx，$\frac{1}{{x}^{2}}$dx．

点评 本题考查了不定积分的分部积分法，属于基础题．

练习册系列答案
相关题目
17．已知定义在R上的奇函数f（x）满足f（x+2）=-f（x），当0≤x≤1时，f（x）=x2，则f（2015）=-1．
18．袋中装有5只乒乓球，其中3只是白球，2只是黄球，先后从袋中无放回地取出两球，则取到1次白球1次黄球的概率是$\frac{3}{5}$．
15．一动圆与圆（x-2）2+y2=1及y轴都相切．则动圆圆心的轨迹是（　　）
A．一点B．两点C．一条抛物线D．两条抛物线
2．直角△ABC的三个顶点都在给定的抛物线y2=4x上，且斜边AB和y轴平行．则△ABC斜边上的高的长度为4．
12．已知椭圆C：x2+$\frac{{y}^{2}}{15}$=1，过C任意一点M作与直线l0：x+y-6=0夹角为30°的直线l，l交l0于点P，则|MP|的最小值是2$\sqrt{2}$．
19．在平面直角坐标系xOy中，圆C1：（x+1）2+（y-6）2=25，圆C2：（x-17）2+（y-30）2=r2，若圆C2上存在一点P，使得过点P可作一条射线与圆C1一次交于点A，B，满足|PA|=2|AB|，则半径r的取值范围是（　　）
A．[5，55]B．[5，50]C．[10，50]D．[10，55]
16．已知定义在R上的函数f（x）=$\frac{-{2}^{x}+a}{{2}^{x+1}+2}$（a为实常数）是奇函数g（x）=2（x-x2）．
（Ⅰ）求a的值，判断并证明函数f（x）的单调性；
（Ⅱ）若对任意的t∈[-1，4]，不等式f（g（t）-1）+f（8t+m）＜0（m为实常数）都成立，求m的取值范围．
（Ⅲ）记F1（x）=f（x）+x2-$\frac{1}{{2}^{x}+1}$+$\frac{1}{2}$，F2（x）=g（x），F3（x）=$\frac{1}{3}$|sin2πx|，b1=$\frac{i}{100}$，i=0，1，2，…，100，若Mk=|Fk（b1）-Fk（b0）|+|Fk（b2）-Fk（b1）|+…+|Fk（b100）-Fk（b99）|，k=1，2，3，试比较M1，M2，M3的大小，并说明理由．
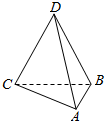17．已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上，△ABC和△DBC所在平面相互垂直，AB=3，AC=$\sqrt{3}$，BC=CD=BD=2$\sqrt{3}$，则球O的表面积为（　　）
A．4πB．12πC．16πD．36π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网