��Ŀ����
5��������$\overrightarrow{a}$=��x1��y1��z1����$\overrightarrow{b}$=��x2��y2��z2������$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$=$\frac{{z}_{1}}{{z}_{2}}$������$\overrightarrow{a}$��$\overrightarrow{b}$���ߵij�ֲ���Ҫ���������� ���ݳ���Ժͱ�Ҫ�ԵĶ���֤���жϼ��ɣ�
��� �⣺������$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$=$\frac{{z}_{1}}{{z}_{2}}$=��
��x1=��x2��y1=��y2��z1=��z2��
��$\overrightarrow{a}$=��x1��y1��z1��=�ˣ�x2��y2��z2��=��$\overrightarrow{b}$��
������$\overrightarrow{a}$��$\overrightarrow{b}$���ߣ�
������x1=0��y2=y1��z2=z1��������$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$=$\frac{{z}_{1}}{{z}_{2}}$����Ҫ�Բ�������
�����dz�ֲ���Ҫ������
���� ���⿼���˳�����Ҫ�������ж����⣬Ҳ�����˿ռ�������Ӧ�����⣬�ǻ�����Ŀ��

��ϰ��ϵ�д�
 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
�����Ŀ
15��һ��Բ��Բ��x-2��2+y2=1��y�ᶼ���У���ԲԲ�ĵĹ켣�ǣ�������
| A�� | һ�� | B�� | ���� | C�� | һ�������� | D�� | ���������� |
17��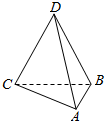 ��֪��ͼ��ʾ������D-ABC���ĸ����������O�������ϣ���ABC�͡�DBC����ƽ�����ֱ��AB=3��AC=$\sqrt{3}$��BC=CD=BD=2$\sqrt{3}$������O�ı����Ϊ��������
��֪��ͼ��ʾ������D-ABC���ĸ����������O�������ϣ���ABC�͡�DBC����ƽ�����ֱ��AB=3��AC=$\sqrt{3}$��BC=CD=BD=2$\sqrt{3}$������O�ı����Ϊ��������
 ��֪��ͼ��ʾ������D-ABC���ĸ����������O�������ϣ���ABC�͡�DBC����ƽ�����ֱ��AB=3��AC=$\sqrt{3}$��BC=CD=BD=2$\sqrt{3}$������O�ı����Ϊ��������
��֪��ͼ��ʾ������D-ABC���ĸ����������O�������ϣ���ABC�͡�DBC����ƽ�����ֱ��AB=3��AC=$\sqrt{3}$��BC=CD=BD=2$\sqrt{3}$������O�ı����Ϊ��������| A�� | 4�� | B�� | 12�� | C�� | 16�� | D�� | 36�� |
14����֪����f��x��=x2+2x+a-1����x�ʣ�-�ޣ�-3��ʱ��f��x����0���������ʵ��a��ȡֵ��Χ�ǣ�������
| A�� | a��-2 | B�� | a��-2 | C�� | a��2 | D�� | a��2 |
15����֪�ⳤΪ4��������ABCD-A1B1C1D1������ΪO����OΪ���ģ�1Ϊ�뾶����P�������ϵ�����һ�㣬��Q��������ABCD-A1B1C1D1�����ϵ�����һ�㣬��$\overrightarrow{PQ}$•$\overrightarrow{DA}$��ȡֵ��ΧΪ��������
| A�� | [-9��9] | B�� | [-12��12] | C�� | [-15��15] | D�� | [-18��18] |