题目内容
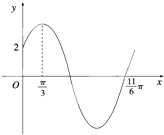 已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<| π |
| 2 |
(1)求f(x)的解析式;
(2)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的
| 1 |
| 2 |
| π |
| 6 |
(3)当x∈[-
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
| 2 |
| π |
| 3 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)由图得到函数的四分之三周期,进一步求得周期,代入周期公式求ω,然后利用五点作图的第二点求得φ,再由f(0)=2求得A的值,则函数解析式可求;
(2)由函数的周期变化和平移变换求得g(x),然后再由简单的复合函数单调性的求法求解g(x)的增区间;
(3)结合(1)中的f(x)的解析式求得y=f(x+
)-
f(x+
),利用三角恒等变换变形后根据x的范围求最值.
(2)由函数的周期变化和平移变换求得g(x),然后再由简单的复合函数单调性的求法求解g(x)的增区间;
(3)结合(1)中的f(x)的解析式求得y=f(x+
| π |
| 12 |
| 2 |
| π |
| 3 |
解答:
解:(1)由图可得,
=
-
=
,
∴T=2π,则ω=
=
=1.
由五点作图的第二点知,1×
+φ=
,则φ=
.
∴f(x)=Asin(x+
),
又f(0)=Asin
=2,得A=4.
∴f(x)=4sin(x+
);
(2)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的
倍所得函数解析式
为y=4sin(2x+
),再将所得函数图象向右平移
个单位,解析式变为y=4sin[2(x-
)+
],
∴g(x)=4sin(2x-
).
由-
+2kπ≤2x-
≤
+2kπ,解得:-
+kπ≤x≤
+kπ,k∈Z.
∴g(x)的单调递增区间为[-
+kπ,
+kπ],k∈Z;
(3)y=f(x+
)-
f(x+
)
=4sin(x+
+
)-4
sin(x+
+
)
=4sin(x+
)-4
cosx
=4sinxcos
+4cosxsin
-4
cosx
=4sin(x-
).
∵x∈[-
,
],
∴x-
∈[-
,
],
∴函数y=f(x+
)-
f(x+
)的最小值为-4,最大值为2.
| 3T |
| 4 |
| 11π |
| 6 |
| π |
| 3 |
| 3π |
| 2 |
∴T=2π,则ω=
| 2π |
| T |
| 2π |
| 2π |
由五点作图的第二点知,1×
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
∴f(x)=Asin(x+
| π |
| 6 |
又f(0)=Asin
| π |
| 6 |
∴f(x)=4sin(x+
| π |
| 6 |
(2)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的
| 1 |
| 2 |
为y=4sin(2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∴g(x)=4sin(2x-
| π |
| 6 |
由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
∴g(x)的单调递增区间为[-
| π |
| 6 |
| π |
| 3 |
(3)y=f(x+
| π |
| 12 |
| 2 |
| π |
| 3 |
=4sin(x+
| π |
| 12 |
| π |
| 6 |
| 2 |
| π |
| 3 |
| π |
| 6 |
=4sin(x+
| π |
| 4 |
| 2 |
=4sinxcos
| π |
| 4 |
| π |
| 4 |
| 2 |
=4sin(x-
| π |
| 4 |
∵x∈[-
| π |
| 2 |
| 5π |
| 12 |
∴x-
| π |
| 4 |
| 3π |
| 4 |
| π |
| 6 |
∴函数y=f(x+
| π |
| 12 |
| 2 |
| π |
| 3 |
点评:本题考查由y=Asin(ωx+φ)型函数的部分图象求解析式,考查复合函数单调区间的求法,训练了三角函数的图象平移及三角恒等变换,是中档题.

练习册系列答案
相关题目
 如图,酒杯的形状为倒立的圆锥,杯深8cm,上口宽6cm,水以20cm2/s的流量倒入杯中,当水深为4cm时,求水面升高的瞬时变化率.
如图,酒杯的形状为倒立的圆锥,杯深8cm,上口宽6cm,水以20cm2/s的流量倒入杯中,当水深为4cm时,求水面升高的瞬时变化率.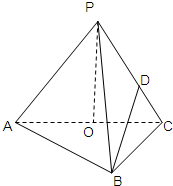 如图,在三棱锥P-ABC,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC. 如图,P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,若PA=
如图,P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,若PA=