题目内容
已知△ABC内接于单位圆,且(1+tanA)(1+tanB)=2,
(1)求角C
(2)求△ABC面积的最大值.
(1)求角C
(2)求△ABC面积的最大值.
考点:两角和与差的正切函数
专题:三角函数的求值
分析:(1)变形已知条件可得tanA+tanB=1-tanA•tanB,代入可得tanC=-tan(A+B)=-
=-1,可得C值;(2)由正弦定理可得c,由余弦定理和基本不等式可得ab得取值范围,进而可得面积的最值.
| tanA+tanB |
| 1-tanAtanB |
解答:
解:(1)∵(1+tanA)(1+tanB)=2
∴tanA+tanB=1-tanA•tanB,
∴tanC=-tan(A+B)=-
=-1,
∴C=
(2)∵△ABC得外接圆为单位圆,
∴其半径R=1
由正弦定理可得c=2RsinC=
,
由余弦定理可得c2=a2+b2-2abcosC,
代入数据可得2=a2+b2+
ab
≥2ab+
ab=(2+
)ab,
∴ab≤
,
∴△ABC得面积S=
absinC≤
•
=
,
∴△ABC面积的最大值为:
∴tanA+tanB=1-tanA•tanB,
∴tanC=-tan(A+B)=-
| tanA+tanB |
| 1-tanAtanB |
∴C=
| 3π |
| 4 |
(2)∵△ABC得外接圆为单位圆,
∴其半径R=1
由正弦定理可得c=2RsinC=
| 2 |
由余弦定理可得c2=a2+b2-2abcosC,
代入数据可得2=a2+b2+
| 2 |
≥2ab+
| 2 |
| 2 |
∴ab≤
| 2 | ||
2+
|
∴△ABC得面积S=
| 1 |
| 2 |
| 1 | ||
2+
|
| ||
| 2 |
| ||
| 2 |
∴△ABC面积的最大值为:
| ||
| 2 |
点评:本题考查两角和与差得正切,涉及正余弦定理和三角形的面积公式,属中档题.

练习册系列答案
相关题目
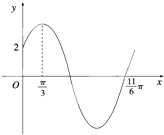 已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<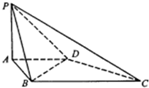 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.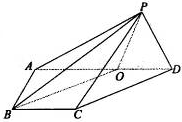 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.