题目内容
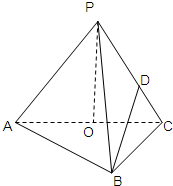如图，在三棱锥P-ABC，AB⊥BC，AB=BC=kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．（1）若k=1，试求异面直线PA与BD所成角余弦值的大小；
（2）当k取何值时，二面角O-PC-B的大小为
| π |
| 3 |
考点：与二面角有关的立体几何综合题,异面直线及其所成的角
专题：空间位置关系与距离
分析：（1）连结OD，由已知条件推导出∠ODB为异面直线PA与BD所成角，由此能求出异面直线PA与BD所成角余弦值的大小．
（2）在面PAC上作OE⊥PC于点E，则∠OEB是二面角O-PC-B的平面角，由此能求出k取
时，二面角O-PC-B的大小为
．
（2）在面PAC上作OE⊥PC于点E，则∠OEB是二面角O-PC-B的平面角，由此能求出k取
2
| ||
| 3 |
| π |
| 3 |
解答：
解：（1）连结OD，∵点O、D分别是AC、PC的中点，
∴OD∥PA，
∴∠ODB为异面直线PA与BD所成角，OD=
PA，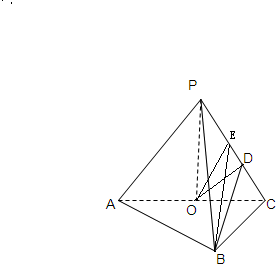
设PA=1，则AB=BC=k=1，OD=
，
∵AB⊥BC，AB=BC，OP⊥底面ABC，D是PC的中点，
∴OB⊥面PAC，
∴OB⊥OD，
又∵AC=
=k
=
，
∴OB=OC=k•
=
，
∴BD=
=
=
，
∴cos∠ODB=
=
．
∴异面直线PA与BD所成角余弦值的大小为
．
（2）在面PAC上作OE⊥PC于点E，
∵OB⊥面PAC，∴∠OEB是二面角O-PC-B的平面角，
PC=PA=1，AB=BC=k，OB=OC=
，
OP=
=
，
∵OP•OC=PC•OE，
∴OE=OP•OC=OP•OB，
∴cot∠OEB=
=OP=
=cot
=
，
∴
=
，解得k=
，
∴k取
时，二面角O-PC-B的大小为
．
∴OD∥PA，
∴∠ODB为异面直线PA与BD所成角，OD=
| 1 |
| 2 |
设PA=1，则AB=BC=k=1，OD=
| 1 |
| 2 |
∵AB⊥BC，AB=BC，OP⊥底面ABC，D是PC的中点，
∴OB⊥面PAC，
∴OB⊥OD，
又∵AC=
| AB2+BC2 |
| 2 |
| 2 |
∴OB=OC=k•
| ||
| 2 |
| ||
| 2 |
∴BD=
| OB2+OD2 |
|
| ||
| 2 |
∴cos∠ODB=
| OD |
| BD |
| ||
| 3 |
∴异面直线PA与BD所成角余弦值的大小为
| ||
| 3 |
（2）在面PAC上作OE⊥PC于点E，
∵OB⊥面PAC，∴∠OEB是二面角O-PC-B的平面角，
PC=PA=1，AB=BC=k，OB=OC=
k
| ||
| 2 |
OP=
| PC2-OC2 |
1-
|
∵OP•OC=PC•OE，
∴OE=OP•OC=OP•OB，
∴cot∠OEB=
| OE |
| OB |
1-
|
| π |
| 3 |
| ||
| 3 |
∴
1-
|
| ||
| 3 |
2
| ||
| 3 |
∴k取
2
| ||
| 3 |
| π |
| 3 |
点评：本题考查异面直线所成角的余弦值的求法，考查二面角为
时k的值的求法，解题时要认真审题，注意空间思维能力的培养．
| π |
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
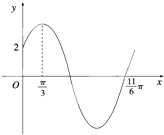已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜