Question

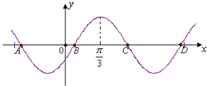已知函数f（x）=sin（ωx+φ）（ω＞0）的部分图象如图所示，点B（

π

12

，0），且在x=

π

3

处取得最大值．
（Ⅰ）若-π＜φ＜π，求φ的值；
（Ⅱ）若φ∈R，图中A，B，C，D中哪些点的横坐标可能为-

φ

ω

．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：计算题,三角函数的图像与性质

分析：（Ⅰ）由图知，

T

4

=

π

4

，从而可求得ω=2，函数f（x）=sin（2x+φ）经过点（

π

3

，1）即可求得φ=2kπ-

π

6

（k∈Z），又-π＜φ＜π，于是可得φ的值；
（Ⅱ）当ωx+φ=2kπ（k∈Z），特别地，k=0时，x=-

φ

ω

，从而可判断图中A，B，C，D中哪些点的横坐标可能为-

φ

ω

．

解答： 解：（I）∵

T

4

=

π

3

-

π

12

=

π

4

，

即

2π

ω

=π，
∴ω=2，
∴f（x）=sin（2x+φ），
把（

π

3

，1）代入上式，得sin（

2π

3

+φ）=1，
∴

2π

3

+φ=2kπ+

π

2

（k∈Z），
∴φ=2kπ-

π

6

（k∈Z），又-π＜φ＜π，
∴φ=-

π

6

；
（II）当ωx+φ=2kπ（k∈Z），
特别地，k=0时，x=-

φ

ω

，
∴点B，D的横坐标可能为-

φ

ω

．

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，确定φ的值是难点，考查识图能力，属于中档题．