Question

若x，y满足

x+y-3≥0 x-y+1≥0 3x-y-5≤0

．求：
（1）z=2x+y的最小值；
（2）z=

y+x

x

的最大值；
（3）z=x²+y²的范围．

Answer 1

考点：简单线性规划

专题：数形结合,不等式的解法及应用

分析：由约束条件作出可行域．
（1）化目标函数为直线方程的斜截式，数形结合求出最优解，得到最优解的坐标，代入目标函数得答案；
（2）由

y+x

x

的几何意义，即可行域内动点与定点连线的斜率求解；
（3）由x²+y²的几何意义，即可行域内动点到原点距离的平方求解．

解答： 解：如图，作出满足已知条件的可行域为△ABC内（及边界）区域，

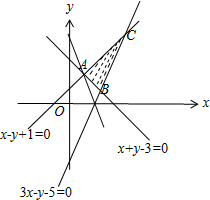
其中A（1，2），B（2，1），C（3，4）．
（1）目标函数z=2x+y，表示直线l：y=-2x+z，z表示该直线纵截距，当l过点A（1，2）时纵截距有最小值，故z_min=4．
（2）目标函数z=

y

x

+1，记k=

y

x

．
则k表示区域中的点与坐标原点连线的斜率，当直线过点A时，斜率最大，
即k_max=2，即zmax=(

y+x

x

)max=3．
（3）目标函数z=x²+y²表示区域内的点到坐标系点的距离的平方，
又原点O到AB的距离d=

|3|

2

=

3 2

2

且垂足是D(

3

2

，

3

2

)在线段AB上，
故OD²≤z≤OC²，即z∈[

9

2

，25]．

点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．