题目内容
已知圆O的方程为(x-1)2+(y+3)2=4.
(Ⅰ)求过点P(2,-1),且与圆O相切的直线l的方程;
(Ⅱ)直线m过点P(2,-l),且与圆O相交于A、B两点,若|AB|=2
,求直线m的方程.
(Ⅰ)求过点P(2,-1),且与圆O相切的直线l的方程;
(Ⅱ)直线m过点P(2,-l),且与圆O相交于A、B两点,若|AB|=2
| 3 |
考点:圆的切线方程,直线与圆的位置关系
专题:直线与圆
分析:(Ⅰ)当直线l的斜率不存在时,直线l的方程为x=2,不成立;当直线l的斜率存在时,设直线l的方程为:kx-y-2k-1=0,则
=2,由此能求出直线l的方程.
(Ⅱ)由圆半径r=2,弦长|AB|=2
,知圆心(1,-3)到直线m的距离d=
=1,由此能求出直线m的方程.
| |k+3-2k-1| | ||
|
(Ⅱ)由圆半径r=2,弦长|AB|=2
| 3 |
| 4-3 |
解答:
解:(Ⅰ)当直线l的斜率不存在时,
直线l的方程为x=2,不成立;
当直线l的斜率存在时,设直线l的方程为:
y+1=k(x-2),即kx-y-2k-1=0,
圆心(1,-3)到直线l的距离d=r=2,
∴
=2,
解得k=
,
∴直线l的方程为y=
(x-2).
(Ⅱ)设直线m的方程为y+1=k1(x-2),即k 1 x-y-2k1-1=0,
∵圆半径r=2,弦长|AB|=2
,
∴圆心(1,-3)到直线m的距离d=
=1,
∴d=
=1,
解得k=
,∴直线m的方程为3x-4y-10=0.
当直线m的斜率不存在时,直线m的方程为x=2,成立.
∴直线m的方程为3x-4y-10=0或x=2.
直线l的方程为x=2,不成立;
当直线l的斜率存在时,设直线l的方程为:
y+1=k(x-2),即kx-y-2k-1=0,
圆心(1,-3)到直线l的距离d=r=2,
∴
| |k+3-2k-1| | ||
|
解得k=
4±2
| ||
| 3 |
∴直线l的方程为y=
4±2
| ||
| 3 |
(Ⅱ)设直线m的方程为y+1=k1(x-2),即k 1 x-y-2k1-1=0,
∵圆半径r=2,弦长|AB|=2
| 3 |
∴圆心(1,-3)到直线m的距离d=
| 4-3 |
∴d=
| |k1+3-2k1-1| | ||
|
解得k=
| 3 |
| 4 |
当直线m的斜率不存在时,直线m的方程为x=2,成立.
∴直线m的方程为3x-4y-10=0或x=2.
点评:本题考查直线方程的求法,是中档题,解题时要认真审题,注意圆的性质和点到直线的距离公式的合理运用.

练习册系列答案
相关题目
函数y=
sinx+cosx(x∈[0,π])的值域是( )
| 3 |
| A、[-2,2] | ||
| B、[-1,2] | ||
| C、[-1,1] | ||
D、[-
|
圆O1:x2+y2+2x-2y=0和圆O2:x2+y2-4x+6y-3=0的位置关系是( )
| A、相离 | B、相交 | C、内切 | D、外切 |
公差不为0的等差数列{an}的第2,3,7项恰为等比数列{bn}的连续三项,则{bn}的公比为( )
| A、1 | B、2 | C、3 | D、4 |
如图对应中,是映射的个数为( )


| A、0 | B、1 | C、2 | D、3 |
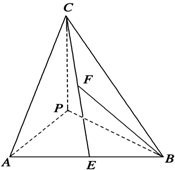 如图,四面体P-ABC中,PA、PB、PC两两垂直,PA=PB=2,PC=4,E是AB的中点,F是CE的中点.
如图,四面体P-ABC中,PA、PB、PC两两垂直,PA=PB=2,PC=4,E是AB的中点,F是CE的中点.