题目内容
已知直线l∥平面α,直线m?平面α,则l与m的位置关系为( )
| A、平行 | B、相交 |
| C、异面 | D、平行或异面 |
考点:空间中直线与平面之间的位置关系
专题:规律型,空间位置关系与距离
分析:根据线面平行的性质定理,即可得出结论.
解答:
解:直线l∥平面α,直线m?平面α,若l,m确定平面,则l∥m,否则l与m异面,
故l与m平行或异面.
故选:D.
故l与m平行或异面.
故选:D.
点评:本题考查线面平行的性质定理,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
已知点O(0,0),A(1,2),B(3,2),以线段AB为直径作圆C,则直线l:x+y-3=0与圆C的位置关系是( )
| A、相交且过圆心 | B、相交但不过圆心 |
| C、相切 | D、相离 |
定义在R上的函数f(x)=e|x|+ln
,且f(x+t)>f(x)在x∈(-1,+∞)上恒成立,则关于x的方程f(2x-1)=f(t)-e的根的个数叙述正确的是( )
| x2+1 |
| A、有两个 | B、有一个 |
| C、没有 | D、上述情况都有可能 |
下列判断正确的是( )
| A、若a∥α,b∥β,α∥β,则a∥b |
| B、a⊥α,b⊥β,α⊥β,则a⊥b |
| C、若a?α,b?β,a∥b,则α∥β |
| D、若m⊥α,m⊥n,则n∥α |
抛物线x2=my上一点M(x0,-3)到焦点的距离为5,则实数m的值为( )
| A、-8 | B、-4 | C、8 | D、4 |
已知点O(0,0),A0(0,1),An(6,7),点A1,A2,…,An-1(n∈N,n≥2)是线段A0An的n等分点,则|
+
+…+
+
|等于( )
| OA0 |
| OA1 |
| OAn-1 |
| OAn |
| A、5n | B、10n |
| C、5(n+1) | D、10(n+1) |
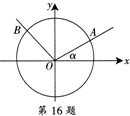 如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A (x1,yl),将射线OA按逆时针方向旋转
如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A (x1,yl),将射线OA按逆时针方向旋转