题目内容
已知向量
=(1,sinx),
=(cos(2x+
),sinx),函数f(x)=
•
(1)求函数f(x)的解析式及其单调递增区间;
(2)在△ABC中,角C为钝角,若f(
)=-
,a=2,c=2
.求△ABC的面积.
| a |
| b |
| π |
| 3 |
| a |
| b |
(1)求函数f(x)的解析式及其单调递增区间;
(2)在△ABC中,角C为钝角,若f(
| C |
| 2 |
| 1 |
| 4 |
| 3 |
考点:平面向量数量积的运算,两角和与差的正弦函数,二倍角的余弦,正弦定理
专题:三角函数的图像与性质,解三角形
分析:(1)由数量积的定义和三角函数的运算易得函数的解析式,再由整体法可求单调递增区间;
(2)结合(1)的结论可求C,由正弦定理可求A,进而由三角形的内角和可得B,然后代入三角形的面积公式可得答案.
(2)结合(1)的结论可求C,由正弦定理可求A,进而由三角形的内角和可得B,然后代入三角形的面积公式可得答案.
解答:
解:(1)f(x)=
•
=cos(2x+
)+sin2x
=cos2xcos
-sin2xsin
+
=
-
sin2x,
由2kπ+
≤2x≤2kπ+
,得:kπ+
≤x≤kπ+
,
所以单调递增区间为[kπ+
,kπ+
],k∈Z …(6分)
(2)∵f(
)=
-
sinC=-
,∴sinC=
又角C为钝角,所以C=
,…(8分)
由正弦定理可得:
=
,解得sinA=
,而0<A<
,
∴A=
,由三角形的内角和可得B=
,…(10分)
∴S△ABC=
acsinB=
×2×2
×
=
. …(12分)
| a |
| b |
| π |
| 3 |
=cos2xcos
| π |
| 3 |
| π |
| 3 |
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
由2kπ+
| π |
| 2 |
| 3π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
所以单调递增区间为[kπ+
| π |
| 4 |
| 3π |
| 4 |
(2)∵f(
| C |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| ||
| 2 |
又角C为钝角,所以C=
| 2π |
| 3 |
由正弦定理可得:
| 2 |
| sinA |
2
| ||
| sinC |
| 1 |
| 2 |
| π |
| 3 |
∴A=
| π |
| 6 |
| π |
| 6 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
点评:本题考查解三角形,涉及平面向量的数量积和三角函数的运算,属中档题.

练习册系列答案
相关题目
已知直线ax+by+c=0,(a,b,c≠0)与圆x2+y2=1相切,则以|a|,|b|,|c|为边( )
| A、不能组成三角形 |
| B、组成锐角三角形 |
| C、组成直角三角形 |
| D、组成钝角三角形 |
已知集合A={(x,y)||x|≤2,|y|≤2,x,y∈Z},集合B={(x,y)|(x-2)2+(y-2)2≤4,x,y∈Z},在集合A中任取一个元素p,则p∈B的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若x2+y2+(λ-1)x+2λy+λ=0表示圆,则λ的取值范围是( )
| A、λ>0 | ||
B、
| ||
C、λ>1或λ<
| ||
| D、λ∈R |
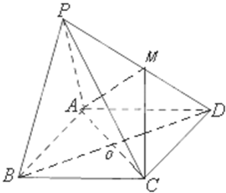 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知 已知函数f(x)=x2-|4x|+3(x∈R),
已知函数f(x)=x2-|4x|+3(x∈R),