题目内容
7.正四棱柱的体对角线长为6.面对角线长为3$\sqrt{3}$,则它的侧面积是36$\sqrt{2}$或18$\sqrt{6}$.分析 列方程组求出正四棱柱的底面边长和高,代入侧面积公式计算.
解答 解:设正四棱柱的底面边长为a,高为b,
则$\left\{\begin{array}{l}{\sqrt{{a}^{2}+{a}^{2}+{b}^{2}}=6}\\{\sqrt{{a}^{2}+{b}^{2}}=3\sqrt{3}}\end{array}\right.$,或$\left\{\begin{array}{l}{\sqrt{{a}^{2}+{a}^{2}+{b}^{2}}=6}\\{\sqrt{{a}^{2}+{a}^{2}}=3\sqrt{3}}\end{array}\right.$,
解得a=3,b=3$\sqrt{2}$,或a=$\frac{3\sqrt{6}}{2}$,b=3.
∴侧面积S=4ab=36$\sqrt{2}$或S=4ab=18$\sqrt{6}$.
故答案为:36$\sqrt{2}$或18$\sqrt{6}$.
点评 本题考查了棱柱的结构特征,侧面积计算,属于中档题.

练习册系列答案
相关题目
19.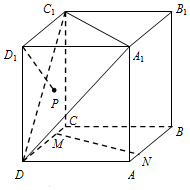 在正方体ABCD-A1B1C1D1中,点M、N分别是直线CD、AB上的动点,点P是△A1C1D内的动点(不包括边界),记直线D1P与MN所成角为θ,若θ的最小值为$\frac{π}{3}$,则点P的轨迹是( )
在正方体ABCD-A1B1C1D1中,点M、N分别是直线CD、AB上的动点,点P是△A1C1D内的动点(不包括边界),记直线D1P与MN所成角为θ,若θ的最小值为$\frac{π}{3}$,则点P的轨迹是( )
 在正方体ABCD-A1B1C1D1中,点M、N分别是直线CD、AB上的动点,点P是△A1C1D内的动点(不包括边界),记直线D1P与MN所成角为θ,若θ的最小值为$\frac{π}{3}$,则点P的轨迹是( )
在正方体ABCD-A1B1C1D1中,点M、N分别是直线CD、AB上的动点,点P是△A1C1D内的动点(不包括边界),记直线D1P与MN所成角为θ,若θ的最小值为$\frac{π}{3}$,则点P的轨迹是( )| A. | 圆的一部分 | B. | 椭圆的一部分 | C. | 抛物线的一部分 | D. | 双曲线的一部分 |
16.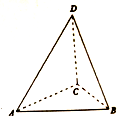 如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )
如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )
 如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )
如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )| A. | $\frac{32π}{3}$ | B. | 4π | C. | 2π | D. | $\frac{4π}{3}$ |
17.某单位招聘员工,有200名应聘者参加笔试,随机抽查了其中20名应聘者笔试试卷,统计他们的成绩如下表:
若按笔试成绩择优录取40名参加面试,由此可预测参加面试的分数线为( )
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) | [90,95) |
| 人数 | 1 | 3 | 6 | 6 | 2 | 1 | 1 |
| A. | 70分 | B. | 75分 | C. | 80分 | D. | 85分 |